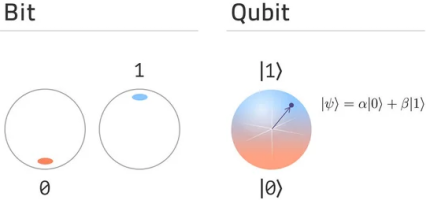
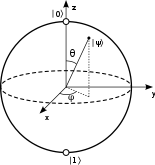
I continue with quantum computing exercises from Quantum Katas. In today’s post, I look at the concept of superposition. I’ll use Julia language with Yao quantum computing simulation package for completing exercises.

Following katas covers the topics on basic single-qubit and multi-qubit gates, superposition, and flow control.

Isotonic (monotonic) regression is the technique of fitting a piecewise line to a sequence of observations such that the fitted line is monotonically non-decreasing.

Let $(x_1,y_1),\ldots ,(x_n,y_n)$ be a given set of observations, where the $y_i \in \mathbb{R}$.

The isotonic regression problem a weighted least-squares fit ${\hat y_i} \approx y_{i}$ for all $i$, subject to the constraint that ${\hat y}_i \leq {\hat y}_j$ whenever $x_i \leq x_j$.

$$ \min \sum_{i=1}^{n} w_i ({\hat y_i}-y_i)^2 \text{ subject to } {\hat y_i} \leq {\hat y_j} {\text{ for all }} (i,j)\in E$$

where $ E={(i,j):x_i \leq x_j} $ specifies the partial ordering of the observed inputs $x_i$.

I continue with quantum computing exercises from Quantum Katas. In this post, I work on qubits and gates exercises. I’ll use Julia language with Yao quantum computing simulation package to complete these tasks.

$$ |0\rangle \otimes |1\rangle = \begin{pmatrix} 1 \ 0 \end{pmatrix} \otimes |1\rangle = \begin{pmatrix} 1 \cdot |1\rangle \ 0 \cdot |1\rangle \end{pmatrix} = \begin{pmatrix} 1 \cdot \begin{pmatrix} 0 \ 1 \end{pmatrix} \ 0 \cdot \begin{pmatrix} 0 \ 1 \end{pmatrix} \end{pmatrix} = \begin{pmatrix} 0 \ 1 \ 0 \ 0 \end{pmatrix} = |01\rangle $$

Following katas use multi-qubit gates. These quantum gates are the quantum counterpart to classical logic gates, acting as the building blocks of quantum algorithms. Quantum gates transform qubit states in various ways, and can be applied sequentially to perform complex quantum calculations.

I continue with quantum computing exercises from Quantum Katas. In this post, I work on qubits and gates exercises. I’ll use Julia language with Yao quantum computing simulation package to complete these tasks.

Following katas use single-qubit gates. These quantum gates are the quantum counterpart to classical logic gates, acting as the building blocks of quantum algorithms. Quantum gates transform qubit states in various ways, and can be applied sequentially to perform complex quantum calculations.

I’ve decided to go thorough the collection of quantum computing exercises Quantum Katas which was created by Microsoft. However, instead of Q# language, I’ll write them in Julia language, and Yao quantum computing library.

The exercises designed to give a basic concepts on quantum computing, and quantum algorithms which include complex number arithmetic, linear algebra, qubits, measurements, and etc.

I’ll start with basic concepts using the Julia language at the beginning, and then gradually introduce features from linear algebra and quantum libraries for more complex exercises.