julia

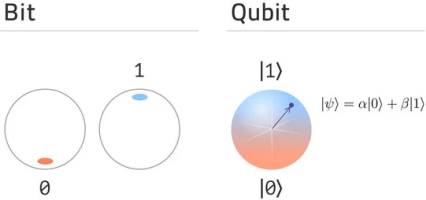
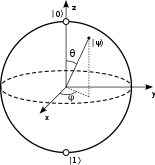
I continue with quantum computing exercises from Quantum Katas. In today’s post, I look at the concept of superposition. I’ll use Julia language with Yao quantum computing simulation package for completing exercises.

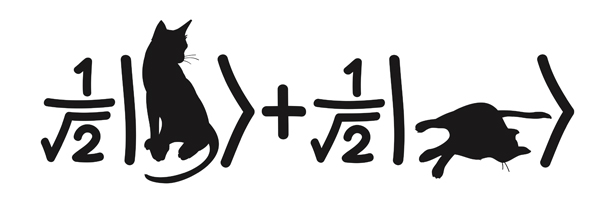
Following katas covers the topics on basic single-qubit and multi-qubit gates, superposition, and flow control.

I continue with quantum computing exercises from Quantum Katas. In this post, I work on qubits and gates exercises. I’ll use Julia language with Yao quantum computing simulation package to complete these tasks.

$$ |0\rangle \otimes |1\rangle = \begin{pmatrix} 1 \ 0 \end{pmatrix} \otimes |1\rangle = \begin{pmatrix} 1 \cdot |1\rangle \ 0 \cdot |1\rangle \end{pmatrix} = \begin{pmatrix} 1 \cdot \begin{pmatrix} 0 \ 1 \end{pmatrix} \ 0 \cdot \begin{pmatrix} 0 \ 1 \end{pmatrix} \end{pmatrix} = \begin{pmatrix} 0 \ 1 \ 0 \ 0 \end{pmatrix} = |01\rangle $$

Following katas use multi-qubit gates. These quantum gates are the quantum counterpart to classical logic gates, acting as the building blocks of quantum algorithms. Quantum gates transform qubit states in various ways, and can be applied sequentially to perform complex quantum calculations.

I continue with quantum computing exercises from Quantum Katas. In this post, I work on qubits and gates exercises. I’ll use Julia language with Yao quantum computing simulation package to complete these tasks.

Following katas use single-qubit gates. These quantum gates are the quantum counterpart to classical logic gates, acting as the building blocks of quantum algorithms. Quantum gates transform qubit states in various ways, and can be applied sequentially to perform complex quantum calculations.

I’ve decided to go thorough the collection of quantum computing exercises Quantum Katas which was created by Microsoft. However, instead of Q# language, I’ll write them in Julia language, and Yao quantum computing library.

The exercises designed to give a basic concepts on quantum computing, and quantum algorithms which include complex number arithmetic, linear algebra, qubits, measurements, and etc.

I’ll start with basic concepts using the Julia language at the beginning, and then gradually introduce features from linear algebra and quantum libraries for more complex exercises.

In statistical learning, many problems require initial preprocessing of multi-dimensional data, and often reduce dimensionality of the data, in a way, to compress features without loosing information about relevant data properties. Common linear dimensionality reduction methods, such as PCA or MDS, in many cases cannot properly reduce data dimensionality especially when data located around nonlinear manifold embedding in high-dimensional space.

There are many nonlinear dimensionality reduction (NLDR) methods for construction of low-dimensional manifold embeddings. A Julia language package ManifoldLearning.jl provides implementation of most common algorithms.