julia

Introduction

The goal of regression is to predict the value of one or more continuous target variables $t$ given the value of a $D$-dimensional vector $x$ of input variables. The polynomial is a specific example of a broad class of functions called linear regression models. The simplest form of linear regression models are also linear functions of the input variables. However, much more useful class of functions can be constructed by taking linear combinations of a fix set of nonlinear functions of the input variables, known as basis functions [1].

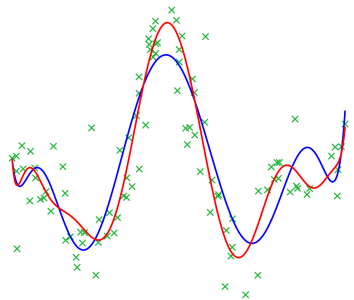
Regression models can be used for time series modeling. Typically, a regression model provides a projection from the baseline status to some relevant demographic variables. Curve-type time series data are quite common examples of these kinds of variables. Typical time series model is the ARMA model. It’s a combination of two types of time series data processes, namely, autoregressive and moving average processes.

Introduction

Stochastic gradient descent (SGD) is a popular stochastic optimization algorithm in the field of machine learning, especially for optimizing deep neural networks. In its core, this iterative algorithm combines two optimization techniques: a stochastic approximation with gradient descent.

SGD is common for optimizing various range of models. We are interested in application of this optimization techniques to standard data science tasks as linear regression and clustering. In addition, we’ll use differentiable programming techniques for simplifying and making versatile our SGD implementation.

Introduction

Symbolic Regression is a type of regression analysis that searches the space of mathematical expressions to find the model that best fits a given dataset, both in terms of accuracy and simplicity. While conventional regression techniques seek to optimize the parameters for a pre-specified model structure, symbolic regression avoids imposing prior assumptions, and instead infers the model from the data. Common representation of the SR model is an expression tree.

• An example of the expression tree for $x^3+x^2+x$

Genetic Programming (GP) evolves computer programs, traditionally represented as expression tree structures. Some of the applications of GP are curve fitting, data modeling, symbolic regression, feature selection, classification, etc.

JuliaCon 2016 Presentation I went to JuliaCon 2016 which happened in Boston. I gave a lightning presentation on the design of the programming environments scheduled to appear in the coming version of Julia language. The project goal was to provide reproducible self-contained environment for any Julia code base. Presentation slides on “Julia Environments” from JuliaCon 2016.

Some time ago, I ported to Julia one of my research projects - linear manifold clustering algorithm or LMCLUS. Initially, it was develop by Robert Haralick, who is my research adviser, and Rave Harpaz in 2005 1. I picked algorithm C++ sources from Rave and created R package with an option to compile into a standalone shared library without R dependencies.