I continue with quantum computing exercises from Quantum Katas. In this post, I work on qubits and gates exercises. I’ll use Julia language with Yao quantum computing simulation package to complete these tasks.

$$ |0\rangle \otimes |1\rangle = \begin{pmatrix} 1 \ 0 \end{pmatrix} \otimes |1\rangle = \begin{pmatrix} 1 \cdot |1\rangle \ 0 \cdot |1\rangle \end{pmatrix} = \begin{pmatrix} 1 \cdot \begin{pmatrix} 0 \ 1 \end{pmatrix} \ 0 \cdot \begin{pmatrix} 0 \ 1 \end{pmatrix} \end{pmatrix} = \begin{pmatrix} 0 \ 1 \ 0 \ 0 \end{pmatrix} = |01\rangle $$

Following katas use multi-qubit gates. These quantum gates are the quantum counterpart to classical logic gates, acting as the building blocks of quantum algorithms. Quantum gates transform qubit states in various ways, and can be applied sequentially to perform complex quantum calculations.

TOC

I’ll start by importing Yao package functionality. I’ll also use SymEngine package to leverage YaoSym functionality, a symbolic computation backend. The symbolic backend may be not very computationally efficient, but it provides better visual output.

using Revise
using Yao
using SymEngine
using YaoPlots, Compose, Cairo

Endianness

The quantum registries of Yao are follow Little-Endian (or least significant bit, LSB) order format for multi-qubit representation, s.t. first qubit as the right-most, and the last qubit is the left-most. The Microsoft Q# defines registries as arrays of qubits which provide Big-Endian order format, a first qubit is stored in right-most location or first element of the array.

The following example shows how to flip qubit state with X gate in multi-qubit system.

q = ket"0000000" # a 7-qubit registry

|0000000⟩

q |> put(7, 1=>X) # flip first qubit

|0000001⟩

q |> put(7, 7=>X) # flip last qubit

|1000001⟩

Example

The following example is reproduced from the Multi-Qubit Systems tutorial.

qs = ket"00"

|00⟩

# an equivalent of Q#: X(qs[0]); H(qs[1]); H(qs[0]); H(qs[1]); CNOT(qs[0], qs[1]);
ch = chain(2, put(2=>X), put(1=>H),  put(2=>H),  put(1=>H), cnot(2,1))
plot(ch) |> PNG();

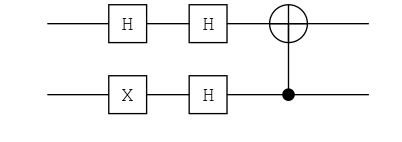
qs |> ch

0.71|00⟩ + -0.71|11⟩

Multi-Qubit Systems

Following exercises come from the Multi-Qubit Systems tutorial. This tutorial covers the following topics:

• Vector representation of multi-qubit systems
• Entangled and separable states
• Dirac notation

Exercise 1: Show that the state is separable

$$ \frac{1}{2}\begin{pmatrix} 1\ i\ -i\ 1 \end{pmatrix} = \begin{pmatrix} ?\ ? \end{pmatrix} \otimes \begin{pmatrix} ? \ ? \end{pmatrix} $$

Answer: $$ \frac{1}{\sqrt{2}}\begin{pmatrix} i\1 \end{pmatrix} \otimes \frac{1}{\sqrt{2}}\begin{pmatrix} -i \ 1 \end{pmatrix} = \begin{pmatrix} i/\sqrt{2} \begin{pmatrix} -i/\sqrt{2} \ 1/\sqrt{2} \end{pmatrix} \ 1/\sqrt{2} \begin{pmatrix} -i/\sqrt{2} \ 1/\sqrt{2} \end{pmatrix} \end{pmatrix} = \begin{pmatrix} 1/2 \ i/2 \ -i/2 \ 1/2 \end{pmatrix} = \frac{1}{2} \begin{pmatrix} 1 \ i \ -i \ 1 \end{pmatrix} $$

Exercise 2: Is this state separable?

$$ \frac{1}{\sqrt{2}}\begin{pmatrix} 1\ 0\ 0\ 1 \end{pmatrix} $$

Answer: No.

Exercise 3: Prepare a basis state

Input: A two-qubit system in the basis state $|00\rangle = \begin{bmatrix} 1 \ 0 \ 0 \ 0 \end{bmatrix}$.

Goal: Transform the system into the basis state $|11\rangle = \begin{bmatrix} 0 \ 0 \ 0 \ 1 \end{bmatrix}$.

ch = chain(2, put(1=>X), put(2=>X))
plot(ch) |> PNG();

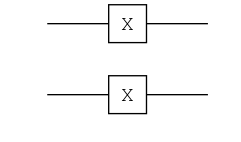
ket"00" |> ch

|11⟩

Exercise 4: Prepare a superposition of two basis states

Input: A two-qubit system in the basis state $|00\rangle = \begin{bmatrix} 1 \ 0 \ 0 \ 0 \end{bmatrix}$.

Goal: Transform the system into the state $\frac{1}{\sqrt2}\big(|00\rangle - |01\rangle\big) = \frac{1}{\sqrt2}\begin{bmatrix} 1 \ -1 \ 0 \ 0 \end{bmatrix}$.

ket"0" * (ket"0" |> X |> H) # tensor decomposition of the goal state

0.71|00⟩ + -0.71|01⟩

ch = chain(2, put(1=>X), put(1=>H))
plot(ch) |> PNG();

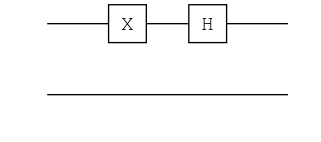
ket"00" |> ch

0.71|00⟩ + -0.71|01⟩

Exercise 5: Prepare a superposition with real amplitudes

Input: A two-qubit system in the basis state $|00\rangle = \begin{bmatrix} 1 \ 0 \ 0 \ 0 \end{bmatrix}$.

Goal: Transform the system into the state $\frac{1}{2}\big(|00\rangle - |01\rangle + |10\rangle - |11\rangle\big) = \frac{1}{2}\begin{bmatrix} 1 \ -1 \ 1 \ -1 \end{bmatrix}$.

(ket"0" |> H)*(ket"0" |> X |>H) # tensor decomposition of the goal state

0.5|00⟩ + -0.5|01⟩ + 0.5|10⟩ + -0.5|11⟩

ch = chain(2, put(2=>H), put(1=>X), put(1=>H))
plot(ch) |> PNG();

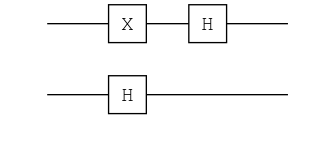
ket"00" |> ch

0.5|00⟩ + -0.5|01⟩ + 0.5|10⟩ + -0.5|11⟩

Exercise 6: Prepare a superposition with complex amplitudes

Input: A two-qubit system in the basis state $|00\rangle = \begin{bmatrix} 1 \ 0 \ 0 \ 0 \end{bmatrix}$.

Goal: Transform the system into the state $\frac{1}{2}\big(|00\rangle + e^{i\pi/4}|01\rangle + e^{i\pi/2}|10\rangle + e^{3i\pi/4}|11\rangle\big) = \frac{1}{2}\begin{bmatrix} 1 \ e^{i\pi/4} \ e^{i\pi/2} \ e^{3i\pi/4} \end{bmatrix}$.

0.5*[1, exp(im*π/4), exp(im*π/2), exp(im*3π/4)] # the goal state

4-element Vector{ComplexF64}:
                   0.5 + 0.0im
    0.3535533905932738 + 0.35355339059327373im
 3.061616997868383e-17 + 0.5im
  -0.35355339059327373 + 0.3535533905932738im

(ket"0" |> H |> S)*(ket"0" |> H |> T) # tensor decomposition of the goal state

0.5|00⟩ + (0.35 + 0.35*im)|01⟩ + 0.5im|10⟩ + (-0.35 + 0.35*im)|11⟩

ch = chain(2, put(1=>H), put(1=>T), put(2=>H), put(2=>S))
plot(ch) |> PNG();

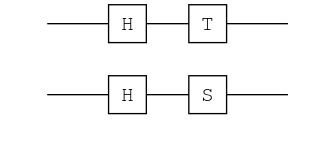
ket"00" |> ch

0.5|00⟩ + (0.35 + 0.35im)|01⟩ + 0.5im|10⟩ + (-0.35 + 0.35im)|11⟩

Multi-Qubit Gates

Following exercises come from Multi-Qubit Gates tutorial.

Exercise 2: Preparing a Bell state

Input: A two-qubit system in the basis state $|00\rangle$.

Goal: Transform the system into the state $\frac{1}{\sqrt{2}}\big(|00\rangle + |11\rangle\big)$.

qs = ket"00"

|00⟩

qs |> chain(2, put(1=>H), cnot(1,2))

0.71|00⟩ + 0.71|11⟩

Exercise 3: Swapping two qubits

Inputs:

1. $N$ qubits in an arbitrary state $|\psi\rangle$, stored in an array of length $N$.
2. Integers index1 and index2 such that $0 \le \text{index1} < \text{index2} \le N - 1$.

Goal: Swap the states of the qubits at the indices given.

ψ = rand_state(4) |> Yao.YaoSym.SymReg
ψ.state .= real.(ψ.state) # remove imaginary parts
ψ

0.0|0000⟩ + 0.04|0001⟩ + 0.15|0010⟩ + -0.18|0011⟩ + 0.08|0100⟩ + -0.01|0101⟩ + 0.08|0110⟩ + -0.04|0111⟩ + -0.1|1000⟩ + 0.12|1001⟩ + -0.14|1010⟩ + -0.03|1011⟩ + 0.28|1100⟩ + 0.09|1101⟩ + -0.01|1110⟩ + 0.39|1111⟩

index1, index2 = 2, 4

(2, 4)

ψ |> control(4, (), (index1,index2)=>SWAP)

0.0|0000⟩ + 0.04|0001⟩ + -0.1|0010⟩ + 0.12|0011⟩ + 0.08|0100⟩ + -0.01|0101⟩ + 0.28|0110⟩ + 0.09|0111⟩ + 0.15|1000⟩ + -0.18|1001⟩ + -0.14|1010⟩ + -0.03|1011⟩ + 0.08|1100⟩ + -0.04|1101⟩ + -0.01|1110⟩ + 0.39|1111⟩

Exercise 4: Controlled Rotation

Inputs:

1. Two qubits in an arbitrary state $|\phi\rangle$, stored as an array of length 2.
2. An angle $\theta$: $-\pi < \theta \leq \pi$.

Goal: Apply a controlled $R_x$ gate, using the first qubit as control and the second qubit as target, with $\theta$ as the angle argument for the gate.

ϕ = ket"00" + ket"10" + ket"01" + ket"11"

|00⟩ + |01⟩ + |10⟩ + |11⟩

θ = π/2

1.5707963267948966

ϕ |> control(2, 1, 2=>Rx(θ))

|00⟩ + (0.71 - 0.71im)|01⟩ + |10⟩ + (0.71 - 0.71im)|11⟩

Exercise 5: Arbitrary Controls

Input:

1. controls - a register of $N$ qubits in an arbitrary state $|\phi\rangle$.
2. target - a qubit in an arbitrary state $|\psi\rangle$.
3. controlBits - an array of $N$ booleans, specifying what state each control qubit should be in order to apply the gate.

Goal: Apply the controlled $X$ gate with the controls as control qubits and target as target, with the state specified by controlBits as controls. If the element of the array is true, the corresponding qubit is a regular control (should be in state $|1\rangle$), and if it is false, the corresponding qubit is an anti-control (should be in state $|0\rangle$).

ϕ = ket"000" + ket"010" + ket"001" + ket"011" + ket"100" + ket"110" + ket"101" + 0.5ket"111"

|000⟩ + |001⟩ + |010⟩ + |011⟩ + |100⟩ + |101⟩ + |110⟩ + 0.5|111⟩

controlBits, target = (1,2), 3

((1, 2), 3)

ϕ |> control(3, controlBits, target=>X)

|000⟩ + |001⟩ + |010⟩ + 0.5|011⟩ + |100⟩ + |101⟩ + |110⟩ + |111⟩

Multi-Qubit Gates (cont.)

Following exercises come from “Part 2: Multi-Qubit Gates” of the Basic quantum computing gates notebook. API reference for multi-qubit manipulations can be found in Yao tutorials and Yao documentaton.

Task 2.1. Two-qubit gate - 1

Input: Two unentangled qubits (stored in an array of length 2). The first qubit will be in state $|\psi\rangle = \alpha |0\rangle + \beta |1\rangle$, the second - in state $|0\rangle$ (this can be written as two-qubit state $\big(\alpha |0\rangle + \beta |1\rangle \big) \otimes |0\rangle = \alpha |00\rangle + \beta |10\rangle$.

Goal: Change the two-qubit state to $\alpha |00\rangle + \beta |11\rangle$.

ψ, ϕ = 0.5ket"0" + 0.3ket"1", ket"0"
ψ, ϕ

(0.5|0⟩ + 0.3|1⟩, |0⟩)

ψ * ϕ |> cnot(2,2,1)

0.5|00⟩ + 0.3|11⟩

Task 2.2. Two-qubit gate - 2

Input: Two unentangled qubits (stored in an array of length 2) in state $|+\rangle \otimes |+\rangle = \frac{1}{2} \big( |00\rangle + |01\rangle + |10\rangle \color{blue}+ |11\rangle \big)$.

Goal: Change the two-qubit state to $\frac{1}{2} \big( |00\rangle + |01\rangle + |10\rangle \color{red}- |11\rangle \big)$.

ψ, ϕ = normalize!(ket"0" + ket"1"), normalize!(ket"0" + ket"1")

(0.71|0⟩ + 0.71|1⟩, 0.71|0⟩ + 0.71|1⟩)

qs = ψ*ϕ 

0.5|00⟩ + 0.5|01⟩ + 0.5|10⟩ + 0.5|11⟩

qs |> control(2, 2, 1=>Z) # or cz(2,2,1) # CZ: control Z gate

0.5|00⟩ + 0.5|01⟩ + 0.5|10⟩ + -0.5|11⟩

Task 2.3. Two-qubit gate - 3

Input: Two unentangled qubits (stored in an array of length 2) in an arbitrary two-qubit state $\alpha |00\rangle + \color{blue}\beta |01\rangle + \color{blue}\gamma |10\rangle + \delta |11\rangle$.

Goal: Change the two-qubit state to $\alpha |00\rangle + \color{red}\gamma |01\rangle + \color{red}\beta |10\rangle + \delta |11\rangle$.

qs = 2ket"00" + 3ket"01" + 4ket"10" + 5ket"11"

2.0|00⟩ + 3.0|01⟩ + 4.0|10⟩ + 5.0|11⟩

copy(qs) |> SWAP # swap(2,2,1)

2.0|00⟩ + 4.0|01⟩ + 3.0|10⟩ + 5.0|11⟩

qs |> chain(2, cnot(1,2), cnot(2,1), cnot(1,2))

2.0|00⟩ + 4.0|01⟩ + 3.0|10⟩ + 5.0|11⟩

Task 2.4. Toffoli gate

Input: Three qubits (stored in an array of length 3) in an arbitrary three-qubit state $\alpha |000\rangle + \beta |001\rangle + \gamma |010\rangle + \delta |011\rangle + \epsilon |100\rangle + \zeta|101\rangle + \color{blue}\eta|110\rangle + \color{blue}\theta|111\rangle$.

Goal: Flip the state of the third qubit if the state of the first two is $|11\rangle$, i.e., change the three-qubit state to $\alpha |000\rangle + \beta |001\rangle + \gamma |010\rangle + \delta |011\rangle + \epsilon |100\rangle + \zeta|101\rangle + \color{red}\theta|110\rangle + \color{red}\eta|111\rangle$.

qs = vcat([ (b+2)*Yao.YaoSym.ket_m(string(b, base=2, pad=3)) for b in Yao.BitBasis.itercontrol(3, [3], (0,)) ],
[ (b+2)*Yao.YaoSym.ket_m(string(b, base=2, pad=3)) for b in Yao.BitBasis.itercontrol(3, [3], (1,)) ]) |> sum

2.0|000⟩ + 3.0|001⟩ + 4.0|010⟩ + 5.0|011⟩ + 6.0|100⟩ + 7.0|101⟩ + 8.0|110⟩ + 9.0|111⟩

qs |> control(3, (2:3), 1=>X)

2.0|000⟩ + 3.0|001⟩ + 4.0|010⟩ + 5.0|011⟩ + 6.0|100⟩ + 7.0|101⟩ + 9.0|110⟩ + 8.0|111⟩

Task 2.5. Fredkin gate

Input: Three qubits (stored in an array of length 3) in an arbitrary three-qubit state $\alpha |000\rangle + \beta |001\rangle + \gamma |010\rangle + \delta |011\rangle + \epsilon |100\rangle + \color{blue}\zeta|101\rangle + \color{blue}\eta|110\rangle + \theta|111\rangle$.

Goal: Swap the states of second and third qubit if and only if the state of the first qubit is $|1\rangle$, i.e., change the three-qubit state to $\alpha |000\rangle + \beta |001\rangle + \gamma |010\rangle + \delta |011\rangle + \epsilon |100\rangle + \color{red}\eta|101\rangle + \color{red}\zeta|110\rangle + \theta|111\rangle$.

qs = vcat([ (b+2)*Yao.YaoSym.ket_m(string(b, base=2, pad=3)) for b in Yao.BitBasis.itercontrol(3, [3], (0,)) ],
[ (b+2)*Yao.YaoSym.ket_m(string(b, base=2, pad=3)) for b in Yao.BitBasis.itercontrol(3, [3], (1,)) ]) |> sum

2.0|000⟩ + 3.0|001⟩ + 4.0|010⟩ + 5.0|011⟩ + 6.0|100⟩ + 7.0|101⟩ + 8.0|110⟩ + 9.0|111⟩

qs |> control(3, 3, (1,2)=>SWAP)

2.0|000⟩ + 3.0|001⟩ + 4.0|010⟩ + 5.0|011⟩ + 6.0|100⟩ + 8.0|101⟩ + 7.0|110⟩ + 9.0|111⟩