I continue with quantum computing exercises from Quantum Katas. In this post, I work on qubits and gates exercises. I’ll use Julia language with Yao quantum computing simulation package to complete these tasks.
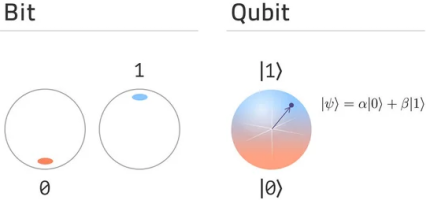
Following katas use single-qubit gates. These quantum gates are the quantum counterpart to classical logic gates, acting as the building blocks of quantum algorithms. Quantum gates transform qubit states in various ways, and can be applied sequentially to perform complex quantum calculations.
TOC
- Example
- Single-Qubit Gates
- Basic Gates Kata
- Task 1.1: State flip: $|0\rangle$ to $|1\rangle$ and vice versa
- Task 1.2. Basis change: $|0\rangle$ to $|+\rangle$ and $|1\rangle$ to $|-\rangle$ (and vice versa)
- Task 1.3. Sign flip: $|+\rangle$ to $|-\rangle$ and vice versa
- Task 1.4. Amplitude change: $|0\rangle$ to $\cos{α} |0\rangle + \sin{α} |1\rangle$
- Task 1.5. Phase flip
- Task 1.6. Phase change
- Task 1.7. Global phase change
- Task 1.8. Bell state change - 1
- Task 1.9. Bell state change - 2
- Task 1.10. Bell state change - 3
I’ll start by importing Yao package functionality. I’ll also use SymEngine package to leverage YaoSym functionality, a symbolic computation backend. The symbolic backend may be not very computationally efficient, but it provides better visual output.
using Yao
using SymEngine
Example
The following example is reproduced from the Qubit notebook.
# q = ArrayReg(bit"0") # another way do describe qubit in Yao
q = ket"0"
|0⟩
state(q) # a state of the qubit represented as vector
2×1 SparseArrays.SparseMatrixCSC{Basic, Int64} with 1 stored entry:
1
⋅
q |> X
|1⟩
q |> H
0.71|0⟩ + -0.71|1⟩
q |> S
0.71|0⟩ + 0.0|1⟩
q |> Rx(2.0)
-0.21|0⟩ + 0.0|1⟩
q |> Ry(1.0)
0.47im|0⟩ + -0.1|1⟩
Single-Qubit Gates
The following exercises come from Single-Qubit Gates tutorial are designed to test your understanding of the quantum gate concepts.
Exercise 1: The gate $Y$
- Input: A qubit in an arbitrary state $|\psi\rangle = \alpha |0\rangle + \beta |1\rangle$
- Goal: Apply the gate $Y$ to the qubit, i.e., transform the given state into $i \alpha |1\rangle - i \beta |0\rangle$.
ψ = 2ket"0" + 3ket"1"
2.0|0⟩ + 3.0|1⟩
ψ |> Y
0.0|0⟩ + 2.0im|1⟩
Exercise 2: Applying a global phase $i$
Input: A qubit in an arbitrary state $|\psi\rangle = \alpha |0\rangle + \beta |1\rangle$
Goal: Use several Pauli gates to change the qubit state to $i|\psi\rangle = i \alpha |0\rangle + i \beta |1\rangle$.
ψ = 2ket"0" + 3ket"1"
2.0|0⟩ + 3.0|1⟩
ψ |> Z |> Y |> X
2.0im|0⟩ + 3.0im|1⟩
Exercise 3: Applying a phase $-1$ to state $|0\rangle$
Input: A qubit in an arbitrary state $|\psi\rangle = \alpha |0\rangle + \beta |1\rangle$
Goal: Use several Pauli gates to change the qubit state to $- \alpha |0\rangle + \beta |1\rangle$.
ψ = 2ket"0" + 3ket"1"
2.0|0⟩ + 3.0|1⟩
ψ |> X |> Z |> X
-2.0|0⟩ + 3.0|1⟩
Exercise 4: Preparing a state $| - \rangle$
Input: A qubit in a state $|0\rangle$
Goal: Transform the qubit into state to $|-\rangle = \frac{1}{\sqrt{2}} \left( |0\rangle - |1\rangle \right)$.
ψ = ket"0"
|0⟩
ψ |> X |> H # or ψ |> H |> Z
0.71|0⟩ + -0.71|1⟩
Exercise 5: Three-fourths phase
Input: A qubit in an arbitrary state $|\psi\rangle = \alpha |0\rangle + \beta |1\rangle$
Goal: Use several phase shift gates to apply the transformation represented by the following matrix to the given qubit: $\begin{bmatrix} 1 & 0 \ 0 & e^{3i \pi /4} \end{bmatrix}$
ψ = 2ket"0" + ket"1"
2.0|0⟩ + |1⟩
ψ |> S |> T
2.0|0⟩ + 0.71im|1⟩
Exercise 6: Preparing a rotated state
Input: Real numbers $\alpha$ and $\beta$ s.t. $\alpha^2 + \beta^2 = 1$, and a qubit in a state $|0\rangle$.
Goal: Use several Pauli gates to change the qubit state to $\alpha |0\rangle - i \beta |1\rangle$.
α, β = cos(π/6), cos(π/3)
(0.8660254037844387, 0.5000000000000001)
α^2 + β^2
1.0000000000000002
ψ = ket"0"
|0⟩
ψ |> Rx(2*atan(β, α))
0.87|0⟩ + 0.0|1⟩
Exercise 7: Preparing an arbitrary state
Input:
- A non-negative real number $\alpha$
- A non-negative real number and $\beta = \sqrt{1-\alpha^2}$
- A real number $\theta$
- A qubit in a state $|0\rangle$
Goal: Use several Pauli gates to change the qubit state to $\alpha |0\rangle + e^{i \theta} \beta |1\rangle$.
α = 0.5
0.5
β = √(1-α^2)
0.8660254037844386
θ = 0.25
0.25
ψ = ket"0"
|0⟩
ψ |> Ry(2*atan(β, α))
0.5|0⟩ + 0.87|1⟩
ψ |> exp(im * θ / 2) * Rz(θ)
0.5|0⟩ + (0.84 + 0.21im)|1⟩
(α)ket"0" + (exp(im * θ)*β)ket"1" # for comparison
0.5|0⟩ + (0.84 + 0.21im)|1⟩
Basic Gates Kata
The following exercises come from Basic quantum computing gates notebook. The exercises covers the following topics:
- basic single-qubit and multi-qubit gates,
- adjoint and controlled gates,
- using gates to modify the state of a qubit.
Task 1.1: State flip: $|0\rangle$ to $|1\rangle$ and vice versa
Input: A qubit in an arbitrary state $|\psi\rangle = \alpha |0\rangle + \beta |1\rangle$
Goal: Change the state of the qubit to $\alpha |1\rangle + \beta |0\rangle$.
ψ = 2ket"0" + 3ket"1"
2.0|0⟩ + 3.0|1⟩
ψ |> X
3.0|0⟩ + 2.0|1⟩
ψ |> X
2.0|0⟩ + 3.0|1⟩
Task 1.2. Basis change: $|0\rangle$ to $|+\rangle$ and $|1\rangle$ to $|-\rangle$ (and vice versa)
Input: A qubit in state $|\psi\rangle = \alpha |0\rangle + \beta |1\rangle$.
Goal: Change the state of the qubit as follows:
- If the qubit is in state $|0\rangle$, change its state to $|+\rangle = \frac{1}{\sqrt{2}} \big(|0\rangle + |1\rangle\big)$.
- If the qubit is in state $|1\rangle$, change its state to $|-\rangle = \frac{1}{\sqrt{2}} \big(|0\rangle - |1\rangle\big)$.
- If the qubit is in superposition, change its state according to the effect on basis vectors.
ψ = ket"0"
|0⟩
ψ |> H
0.71|0⟩ + 0.71|1⟩
ψ = ket"1"
|1⟩
ψ |> H
0.71|0⟩ + -0.71|1⟩
ψ = 0.5ket"0" + 0.86ket"1"
0.5|0⟩ + 0.86|1⟩
ψ |> H
0.96|0⟩ + -0.25|1⟩
Task 1.3. Sign flip: $|+\rangle$ to $|-\rangle$ and vice versa.
Input: A qubit in state $|\psi\rangle = \alpha |0\rangle + \beta |1\rangle$.
Goal : Change the qubit state to $\alpha |0\rangle - \beta |1\rangle$ (flip the sign of $|1\rangle$ component of the superposition).
ψ = 2ket"0" + 3ket"1"
2.0|0⟩ + 3.0|1⟩
ψ |> Z
2.0|0⟩ + -3.0|1⟩
Task 1.4. Amplitude change: $|0\rangle$ to $\cos{α} |0\rangle + \sin{α} |1\rangle$.
Inputs:
- Angle $\alpha$, in radians, represented as Double.
- A qubit in state $|\psi\rangle = \beta |0\rangle + \gamma |1\rangle$.
Goal: Change the state of the qubit as follows:
- If the qubit is in state $|0\rangle$, change its state to $\cos{α} |0\rangle + \sin{α} |1\rangle$.
- If the qubit is in state $|1\rangle$, change its state to $-\sin{α} |0\rangle + \cos{α} |1\rangle$.
- If the qubit is in superposition, change its state according to the effect on basis vectors.
α = deg2rad(30)
0.5235987755982988
cos(α), sin(α)
(0.8660254037844387, 0.49999999999999994)
ψ = ket"0"
|0⟩
ψ |> Ry(2α)
0.87|0⟩ + 0.5|1⟩
ψ = ket"1"
|1⟩
ψ |> Ry(2α)
-0.5|0⟩ + 0.87|1⟩
ψ = sin(α)ket"0" + cos(α)ket"1"
0.5|0⟩ + 0.87|1⟩
ψ |> Ry(2α)
|1⟩
Task 1.5. Phase flip
Input: A qubit in state $|\psi\rangle = \alpha |0\rangle + \beta |1\rangle$.
Goal: Change the qubit state to $\alpha |0\rangle + \color{red}i\beta |1\rangle$ (add a relative phase $i$ to $|1\rangle$ component of the superposition).
ψ = sin(α)ket"0" + cos(α)ket"1"
0.5|0⟩ + 0.87|1⟩
ψ |> S
0.5|0⟩ + 0.87im|1⟩
Task 1.6. Phase change
Inputs:
- Angle $\alpha$, in radians, represented as Double.
- A qubit in state $|\psi\rangle = \beta |0\rangle + \gamma |1\rangle$.
Goal: Change the state of the qubit as follows:
- If the qubit is in state $|0\rangle$, don’t change its state.
- If the qubit is in state $|1\rangle$, change its state to $e^{i\alpha} |1\rangle$.
- If the qubit is in superposition, change its state according to the effect on basis vectors: $\beta |0\rangle + \color{red}{e^{i\alpha}} \gamma |1\rangle$.
α = deg2rad(30)
0.5235987755982988
ψ = ket"0"
|0⟩
R1(θ) = exp(im * θ / 2) * Rz(θ) # a phase shift gate [1 0; 0 exp(iθ)]
R1(α) |> mat
2×2 LinearAlgebra.Diagonal{ComplexF64, Vector{ComplexF64}}:
1.0+0.0im ⋅
⋅ 0.866025+0.5im
ψ |> R1(α)
|0⟩
ψ = ket"1"
|1⟩
ψ |> R1(α)
(0.87 + 0.5im)|1⟩
ψ = ket"0" + ket"1"
|0⟩ + |1⟩
ψ |> R1(α)
|0⟩ + (0.87 + 0.5im)|1⟩
Task 1.7. Global phase change
Input: A qubit in state $|\psi\rangle = \beta |0\rangle + \gamma |1\rangle$.
Goal: Change the state of the qubit to $- \beta |0\rangle - \gamma |1\rangle$.
ψ = sin(α)ket"0" + cos(α)ket"1"
0.5|0⟩ + 0.87|1⟩
ψ |> rot(igate(1), 2π)
-0.5|0⟩ + -0.87|1⟩
Task 1.8. Bell state change - 1
Input: Two entangled qubits in Bell state $|\Phi^{+}\rangle = \frac{1}{\sqrt{2}} \big(|00\rangle + |11\rangle\big)$.
Goal: Change the two-qubit state to $|\Phi^{-}\rangle = \frac{1}{\sqrt{2}} \big(|00\rangle - |11\rangle\big)$.
Φ = normalize!(ket"00" + ket"11")
0.71|00⟩ + 0.71|11⟩
Φ |> chain(2, put(1=>Z)) # or Φ |> chain(2, put(2=>Z))
0.71|00⟩ + -0.71|11⟩
Task 1.9. Bell state change - 2
Input: Two entangled qubits in Bell state $|\Phi^{+}\rangle = \frac{1}{\sqrt{2}} \big(|00\rangle + |11\rangle\big)$.
Goal: Change the two-qubit state to $|\Psi^{+}\rangle = \frac{1}{\sqrt{2}} \big(|01\rangle + |10\rangle\big)$.
Φ = normalize!(ket"00" + ket"11")
0.71|00⟩ + 0.71|11⟩
Φ |> chain(2, put(2=>X)) # or Φ |> chain(2, put(1=>X))
0.71|01⟩ + 0.71|10⟩
Task 1.10. Bell state change - 3
Input: Two entangled qubits in Bell state $|\Phi^{+}\rangle = \frac{1}{\sqrt{2}} \big(|00\rangle + |11\rangle\big)$.
Goal: Change the two-qubit state, without adding a global phase, to $|\Psi^{-}\rangle = \frac{1}{\sqrt{2}} \big(|01\rangle - |10\rangle\big)$.
Φ = normalize!(ket"00" + ket"11")
0.71|00⟩ + 0.71|11⟩
Φ |> chain(2, put(1=>Y), put(2=>rot(igate(1), π)))
0.71|01⟩ + -0.71|10⟩