Quantum Computing Katas: Superposition

I continue with quantum computing exercises from Quantum Katas. In today’s post, I look at the concept of superposition. I’ll use Julia language with Yao quantum computing simulation package for completing exercises.

cat

Following katas covers the topics on basic single-qubit and multi-qubit gates, superposition, and flow control.

Simple Gates
Arbitrary Rotations

I'll start by importing `Yao` package functionality. I'll also use `SymEngine` package to leverage `YaoSym` functionality, a symbolic computation backend. The symbolic backend may be not very computationally efficient, but it provides better visual output.

using Yao
using SymEngine
using YaoPlots, Compose, Cairo

Simple Gates

Following exercises come from the Multi-Qubit Systems tutorial. This tutorial covers the following topics:

Vector representation of multi-qubit systems
Entangled and separable states
Dirac notation

Task 1.1. Plus state

Input: A qubit in the $|0\rangle$ state.

Goal: Change the state of the qubit to $|+\rangle = \frac{1}{\sqrt{2}} \big(|0\rangle + |1\rangle\big)$.

ket"0" |> H

0.71|0⟩ + 0.71|1⟩

Task 1.2. Minus state

Input: A qubit in the $|0\rangle$ state.

Goal: Change the state of the qubit to $|-\rangle = \frac{1}{\sqrt{2}} \big(|0\rangle - |1\rangle\big)$.

ket"0" |> X |> H

0.71|0⟩ + -0.71|1⟩

Task 1.3. Superposition of all basis vectors on two qubits

Input: Two qubits in the $|00\rangle$ state.

Goal: Change the state of the qubits to $|+\rangle \otimes |+\rangle = \frac{1}{2} \big(|00\rangle + |01\rangle + |10\rangle + |11\rangle\big)$.

ket"00" |> chain(2, put(1=>H), put(2=>H))

0.5|00⟩ + 0.5|01⟩ + 0.5|10⟩ + 0.5|11⟩

Task 1.4. Superposition of basis vectors with phase flip

Input: Two qubits in the $|00\rangle$ sate.

Goal: Change the state of the qubits to $\frac{1}{2}\big(|00\rangle+|01\rangle+|10\rangle-|11\rangle \big)$.

ch = chain(2, put(1=>H), put(2=>H), control(2, 1=>Z))
plot(ch) |> PNG();

png

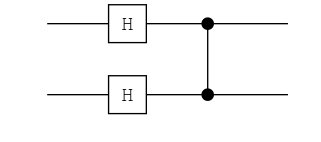
ket"00" |> ch

0.5|00⟩ + 0.5|01⟩ + 0.5|10⟩ + -0.5|11⟩

Task 1.5. Superposition of basis vectors with phases

Input: Two qubits in the $|00\rangle$ state.

Goal: Change the state of the qubits to $\frac{1}{2} \big(|00\rangle + i|01\rangle - |10\rangle - i|11\rangle\big)$.

ch = chain(2, put(1=>H), put(2=>H), put(1=>S), put(2=>Z))
plot(ch) |> PNG();

png

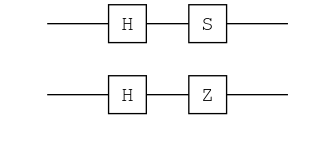
ket"00" |> ch

0.5|00⟩ + 0.5im|01⟩ + -0.5|10⟩ + -0.5im|11⟩

Task 1.6. Bell state $|\Phi^{+}\rangle$

Input: Two qubits in the $|00\rangle$ state.

Goal: Change the state of the qubits to $|\Phi^{+}\rangle = \frac{1}{\sqrt{2}} \big (|00\rangle + |11\rangle\big)$.

ch = chain(2, put(2=>H), cnot(2, 1))
plot(ch) |> PNG();

png

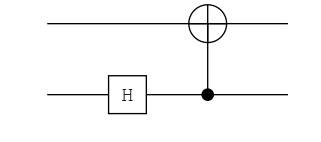
ket"00" |> ch

0.71|00⟩ + 0.71|11⟩

Task 1.7. All Bell states

Inputs:

Two qubits in the $|00\rangle$ state.
An integer index.

Goal: Change the state of the qubits to one of the Bell states.

# State: Φ⁺
ch = chain(2, put(2=>H), cnot(2, 1))
plot(ch) |> PNG();

png

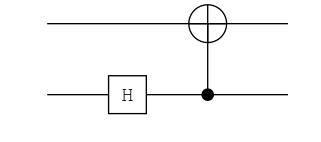
ket"00" |> ch

0.71|00⟩ + 0.71|11⟩

# State: Φ⁻
ch = chain(2, put(2=>H), put(2=>Z), cnot(2, 1))
plot(ch) |> PNG();

png

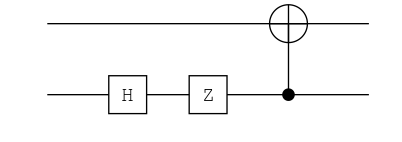
ket"00" |> ch

0.71|00⟩ + -0.71|11⟩

# State: Ψ⁺
ch = chain(2, put(2=>H), put(1=>X), cnot(2, 1))
plot(ch) |> PNG();

png

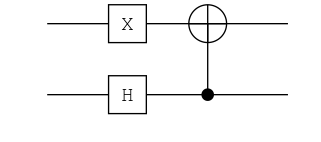
ket"00" |> ch

0.71|01⟩ + 0.71|10⟩

# State: Ψ⁻
ch = chain(2, put(2=>H), put(2=>Z), put(1=>X), cnot(2, 1))
plot(ch) |> PNG();

png

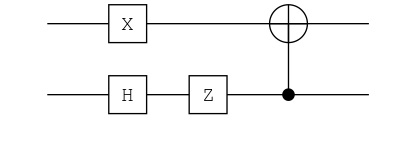
ket"00" |> ch

0.71|01⟩ + -0.71|10⟩

Now put it all together as follows

function bellstates(idx)
    ch = chain(2, put(2=>H))
    if idx == 2
        ch = chain(2, ch..., put(2=>Z))
    elseif idx == 3
        ch = chain(2, ch..., put(1=>X))
    elseif idx == 4
        ch = chain(2, ch..., put(2=>Z), put(1=>X))
    end
    chain(2, ch..., cnot(2, 1))
end

bellstates (generic function with 1 method)

[i => (copy(ket"00") |> bellstates(i)) for i in 1:4]

4-element Vector{Pair{Int64, ArrayReg{2, Basic, SparseArrays.SparseMatrixCSC{Basic, Int64}}}}:
 1 => 0.71|00⟩ + 0.71|11⟩
 2 => 0.71|00⟩ + -0.71|11⟩
 3 => 0.71|01⟩ + 0.71|10⟩
 4 => 0.71|01⟩ + -0.71|10⟩

Task 1.8. Greenberger–Horne–Zeilinger state

Input: $N$ ($N \ge 1$) qubits in the $|0 \dots 0\rangle$ state (stored in an array of length $N$).

Goal: Change the state of the qubits to the GHZ state $\frac{1}{\sqrt{2}} \big (|0\dots0\rangle + |1\dots1\rangle\big)$.

ghz(n) = chain(n, put(1=>H), (cnot(1, i) for i in 2:n)...)

ghz (generic function with 1 method)

ch = ghz(3)
plot(ch) |> PNG();

png

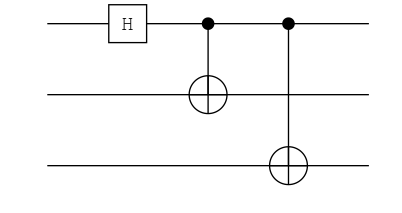
n = 7
zero_state(Basic, n) |> ghz(n)

0.71|0000000⟩ + 0.71|1111111⟩

Task 1.9. Superposition of all basis vectors

Input: $N$ ($N \ge 1$) qubits in the $|0 \dots 0\rangle$ state.

Goal: Change the state of the qubits to an equal superposition of all basis vectors $\frac{1}{\sqrt{2^N}} \big (|0 \dots 0\rangle + \dots + |1 \dots 1\rangle\big)$.

basis(n) = repeat(n, H)

basis (generic function with 1 method)

ch = basis(3)
plot(ch) |> PNG();

png

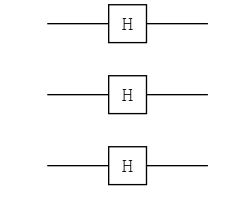
n = 4
zero_state(Basic, n) |> basis(n)

0.25|0000⟩ + 0.25|0001⟩ + 0.25|0010⟩ + 0.25|0011⟩ + 0.25|0100⟩ + 0.25|0101⟩ + 0.25|0110⟩ + 0.25|0111⟩ + 0.25|1000⟩ + 0.25|1001⟩ + 0.25|1010⟩ + 0.25|1011⟩ + 0.25|1100⟩ + 0.25|1101⟩ + 0.25|1110⟩ + 0.25|1111⟩

Task 1.10. Superposition of all even or all odd numbers

Inputs:

$N$ ($N \ge 1$) qubits in the $|0 \dots 0\rangle$ state (stored in an array of length $N$).
A boolean isEven.

Goal: Prepare a superposition of all even numbers if isEven is true, or of all odd numbers if isEven is false.

A basis state encodes an integer number using big-endian binary notation: state $|01\rangle$ corresponds to the integer $1$, and state $|10 \rangle$ - to the integer $2$.

For example, for $N = 2$ and isEven = false you need to prepare superposition $\frac{1}{\sqrt{2}} \big (|01\rangle + |11\rangle\big )$,
and for $N = 2$ and isEven = true - superposition $\frac{1}{\sqrt{2}} \big (|00\rangle + |10\rangle\big )$.

function allEven(isEven, n)
    ch = chain(n, repeat(H, 2:n))
    isEven ? ch : push!(ch, put(1=>X))
end

allEven (generic function with 1 method)

zero_state(Basic, 3) |> allEven(true, 3)

0.5|000⟩ + 0.5|010⟩ + 0.5|100⟩ + 0.5|110⟩

zero_state(Basic, 4) |> allEven(false, 4)

0.35|0001⟩ + 0.35|0011⟩ + 0.35|0101⟩ + 0.35|0111⟩ + 0.35|1001⟩ + 0.35|1011⟩ + 0.35|1101⟩ + 0.35|1111⟩

Task 1.11. Superposition of $|0 \dots 0\rangle$ and the given bit string

Inputs:

$N$ ($N \ge 1$) qubits in the $|0 \dots 0\rangle$ state.
A bit string of length $N$ represented as Bool[]. Bit values false and true correspond to $|0\rangle$ and $|1\rangle$ states. You are guaranteed that the first bit of the bit string is true.

Goal: Change the state of the qubits to an equal superposition of $|0 \dots 0\rangle$ and the basis state given by the bit string.

For example, for the bit string [true, false] the state required is $\frac{1}{\sqrt{2}}\big(|00\rangle + |10\rangle\big)$.

function BitStringSuperposition(bits)
    n = length(bits)
    ch = chain(n, put(n=>H), (cnot(n, i) for i in 1:n-1 if bits[i] == 1)...)
    zero_state(Basic, n) |> ch
end

BitStringSuperposition (generic function with 1 method)

BitStringSuperposition(bit"10")

0.71|00⟩ + 0.71|10⟩

BitStringSuperposition(bit"101")

0.71|000⟩ + 0.71|101⟩

BitStringSuperposition(bit"10101")

0.71|00000⟩ + 0.71|10101⟩

Task 1.12. Superposition of two bit strings

Inputs:

$N$ ($N \ge 1$) qubits in the $|0 \dots 0\rangle$ state.
Two bit strings of length $N$. Bit values false and true correspond to $|0\rangle$ and $|1\rangle$ states. You are guaranteed that the two bit strings differ in at least one bit.

Goal: Change the state of the qubits to an equal superposition of the basis states given by the bit strings.

For example, for bit strings [false, true, false] and [false, false, true] the state required is $\frac{1}{\sqrt{2}}\big(|010\rangle + |001\rangle\big)$.

function TwoBitStringSuperposition(bs1, bs2)    
    # initialize 
    n = length(bs1)
    @assert n == length(bs2) "Bit string must be of the same length"
    qs = zero_state(Basic, n)
    ch = chain(n)
    
    # find position of first difference 
    diff = Yao.BitBasis.baddrs(xor(bs1, bs2))  
    
    
    # apply H gate to corresponding qubit to create superposition
    j = 0
    if length(diff) > 0
        j = first(diff)
        push!(ch, put(j=>H))
    end
    
    for i in 1:n        
        if bs1[i] == bs2[i] && bs1[i] == 1
            # if two bits are the same, apply X gate
            push!(ch, put(i=>X))
        elseif i > j
            # if two bits are different, set their difference using CNOT gate
            push!(ch, cnot(j, i))
            bs1[i] != bs1[j] && push!(ch, put(i=>X))
        end
    end
    qs |> ch, plot(ch) |> PNG()
end

TwoBitStringSuperposition (generic function with 1 method)

TwoBitStringSuperposition(bit"0110", bit"1011")

png

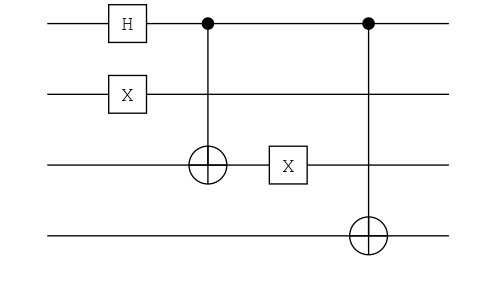
(0.71|0110⟩ + 0.71|1011⟩, false)

Arbitrary Rotations

Task 2.1. Unequal superposition

Inputs:

A qubit in the $|0\rangle$ state.
Angle $\alpha$, in radians, represented as Double.

Goal : Change the state of the qubit to $\cos{α} |0\rangle + \sin{α} |1\rangle$.

α = π/4

0.7853981633974483

cos(α)*ket"0" + sin(α)*ket"1"

0.71|0⟩ + 0.71|1⟩

ket"0" |> Ry(2*α)

0.71|0⟩ + 0.71|1⟩

Task 2.2. $\frac{1}{\sqrt{2}}|00\rangle+\frac{1}{2}|10\rangle+\frac{1}{2}|11\rangle$ state

Input: Two qubits in the $|00\rangle$ state.

Goal: Change the state of the qubits to $\frac{1}{\sqrt{2}}|00\rangle+\frac{1}{2}|10\rangle+\frac{1}{2}|11\rangle$.

ch = chain(2, put(1=>H), control(1, 2=>H))
plot(ch) |> PNG();

png

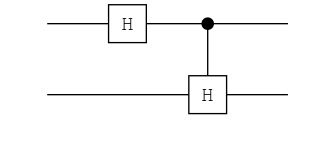
ket"00" |> ch

0.71|00⟩ + 0.5|01⟩ + 0.5|11⟩

Task 2.3. $\frac{1}{\sqrt{3}} \big(|00\rangle + |01\rangle + |10\rangle\big)$ state

Input: Two qubits in the $|00\rangle$ state.

Goal: Change the state of the qubits to $\frac{1}{\sqrt{3}} \big(|00\rangle + |01\rangle + |10\rangle\big)$.

θ₁ = π/4
θ₂ = 2asin(sqrt(1/3))
ch23 = chain(2, put(1=>Ry(θ₁)), put(2=>Ry(θ₂)), put(2=>X), control(2,1=>X), put(1=>Ry(-θ₁)), put(2=>X))
plot(ch23) |> PNG();
ch23 = chain(2, put(2=>Ry(θ₂)), put(2=>X), control(2,1=>H), put(2=>X))
plot(ch23) |> PNG();

png

ket"00" |> ch23

0.58|00⟩ + 0.58|01⟩ + 0.58|10⟩

1/sqrt(3)*(ket"00" + ket"01" + ket"10")

0.58|00⟩ + 0.58|01⟩ + 0.58|10⟩

Task 2.4. $\frac{1}{\sqrt{3}} \big( |00\rangle + \omega |01\rangle + \omega^2 |10\rangle \big)$ state

Input: Two qubits in $|0\rangle$ state (stored in an array of length 2).

Output: Change the state of the qubits to $\frac{1}{\sqrt{3}} \big( |00\rangle + \omega |01\rangle + \omega^2 |10\rangle \big)$ where $\omega = e^{2\pi i/3}$.

ch24 = copy(ch23) # copy chain from previous exercise (#2.3)
R1(θ) = exp(im * θ / 2) * Rz(θ)
# add the relative phases to both |01⟩ and |10⟩ basis states
# without changing the |00⟩ state
push!(ch24, put(1 => R1(2π/3)))
push!(ch24, put(2 => R1(4π/3)))
plot(ch24) |> PNG();

png

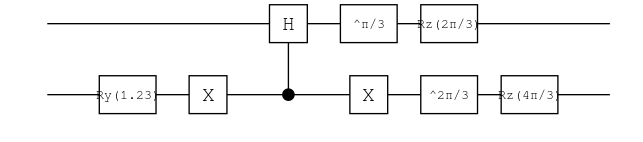
ket"00" |> ch24

0.58|00⟩ + (-0.29 + 0.5*im)|01⟩ + (-0.29 - 0.5im)|10⟩

ω = exp(im * 2π/3)
1/sqrt(3)*(ket"00" + ω*ket"01" + ω^2*ket"10")

0.58|00⟩ + (-0.29 + 0.5im)|01⟩ + (-0.29 - 0.5im)|10⟩

Task 2.5. Hardy state

Input: Two qubits in the $|00\rangle$ state.

Goal: Change the state of the qubits to $\frac{1}{\sqrt{12}} \big(3|00\rangle + |01\rangle + |10\rangle + |11\rangle\big)$.

θ₁ = 2acos(sqrt(10/12))
ch25 = chain(2, put(2=>Ry(θ₁)))
θ₂ = 2acos(sqrt(9/10))
ch25_2 = chain(2, put(2 => X), control(2,1=>Ry(θ₂)), put(2 => X))
append!(ch25, ch25_2)
ch25_3 = chain(2, control(2,1=>Ry(2π/4)))
append!(ch25, ch25_3)
plot(ch25) |> PNG();

png

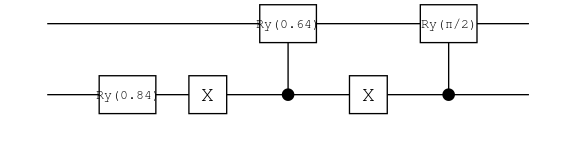
ket"00" |> ch25

0.87|00⟩ + 0.29|01⟩ + 0.29|10⟩ + 0.29|11⟩

1/sqrt(12)*(3ket"00" + ket"01" + ket"10"+ ket"11")

0.87|00⟩ + 0.29|01⟩ + 0.29|10⟩ + 0.29|11⟩

Table of Contents

Simple Gates

Task 1.1. Plus state

Task 1.2. Minus state

Task 1.3. Superposition of all basis vectors on two qubits

Task 1.4. Superposition of basis vectors with phase flip

Task 1.5. Superposition of basis vectors with phases

Task 1.6. Bell state $|\Phi^{+}\rangle$

Task 1.7. All Bell states

Task 1.8. Greenberger–Horne–Zeilinger state

Task 1.9. Superposition of all basis vectors

Task 1.10. Superposition of all even or all odd numbers

Task 1.11. Superposition of $|0 \dots 0\rangle$ and the given bit string

Task 1.12. Superposition of two bit strings

Arbitrary Rotations

Task 2.1. Unequal superposition

Task 2.2. $\frac{1}{\sqrt{2}}|00\rangle+\frac{1}{2}|10\rangle+\frac{1}{2}|11\rangle$ state

Task 2.3. $\frac{1}{\sqrt{3}} \big(|00\rangle + |01\rangle + |10\rangle\big)$ state

Task 2.4. $\frac{1}{\sqrt{3}} \big( |00\rangle + \omega |01\rangle + \omega^2 |10\rangle \big)$ state

Task 2.5. Hardy state