clustering

In statistical learning, many problems require initial preprocessing of multi-dimensional data, and often reduce dimensionality of the data, in a way, to compress features without loosing information about relevant data properties. Common linear dimensionality reduction methods, such as PCA or MDS, in many cases cannot properly reduce data dimensionality especially when data located around nonlinear manifold embedding in high-dimensional space.

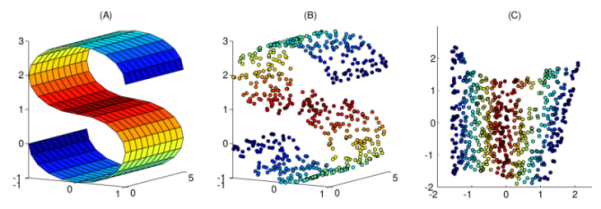
There are many nonlinear dimensionality reduction (NLDR) methods for construction of low-dimensional manifold embeddings. A Julia language package ManifoldLearning.jl provides implementation of most common algorithms.

Introduction

Stochastic gradient descent (SGD) is a popular stochastic optimization algorithm in the field of machine learning, especially for optimizing deep neural networks. In its core, this iterative algorithm combines two optimization techniques: a stochastic approximation with gradient descent.

SGD is common for optimizing various range of models. We are interested in application of this optimization techniques to standard data science tasks as linear regression and clustering. In addition, we’ll use differentiable programming techniques for simplifying and making versatile our SGD implementation.

Some time ago, I ported to Julia one of my research projects - linear manifold clustering algorithm or LMCLUS. Initially, it was develop by Robert Haralick, who is my research adviser, and Rave Harpaz in 2005 1. I picked algorithm C++ sources from Rave and created R package with an option to compile into a standalone shared library without R dependencies.