An autoencoder is a type of a neural network used to learn, in an unsupervised way, a compressed data representation by matching its input to its output. An efficient compression is archived by minimizing the reconstruction error.
 |
| Michela Massi, CC BY-SA 4.0, via Wikimedia Commons |
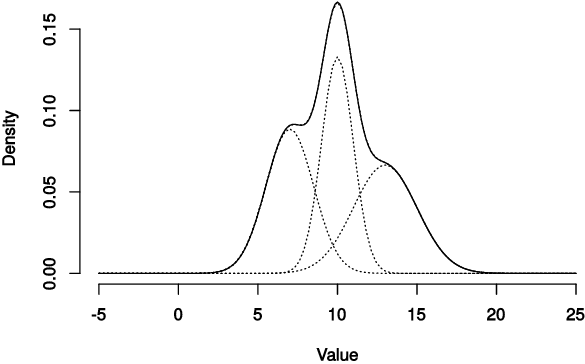
Mixture models are used for many purposes in data science, e.g. to represent feature distributions or spatial relations. Given a fixed data sample, one can fit a mixture model to it using one of a variety of methods. A very common mixture structure is based on Gaussian distributions, the Gaussian Mixture Model (GMM). The expectation-minimization (EM) algorithm allows to find GMM parameters by maximizing model’s likelihood. This approach usually requires closed-form description of parameters’ estimates and have slow convergence to optimal solution. These limitation can be overcome by using (quasi-)Newton optimization. In conjunction with automatic differentiation (AD), finding optimal model parameters become trivial.
For modeling a collection of time series, another model based on a mixture of ARMA processes, Mixture of ARMA Models, can be used. Using similar MLE optimization and AD approach, we will show how to cluster time series.
Read More