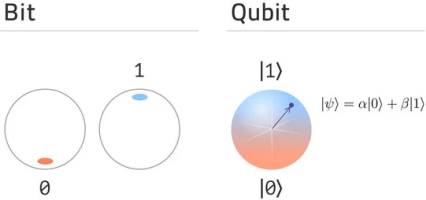
I continue with quantum computing exercises from Quantum Katas. In this post, I work on qubits and gates exercises. I’ll use Julia language with Yao quantum computing simulation package to complete these tasks.
$$
|0\rangle \otimes |1\rangle = \begin{pmatrix} 1 \ 0 \end{pmatrix} \otimes |1\rangle =
\begin{pmatrix} 1 \cdot |1\rangle \ 0 \cdot |1\rangle \end{pmatrix} =
\begin{pmatrix} 1 \cdot \begin{pmatrix} 0 \ 1 \end{pmatrix} \ 0 \cdot \begin{pmatrix} 0 \ 1 \end{pmatrix} \end{pmatrix} = \begin{pmatrix} 0 \ 1 \ 0 \ 0 \end{pmatrix} = |01\rangle
$$
Following katas use multi-qubit gates. These quantum gates are the quantum counterpart to classical logic gates, acting as the building blocks of quantum algorithms. Quantum gates transform qubit states in various ways, and can be applied sequentially to perform complex quantum calculations.
Read More