Probability

Outline

Events and their probabilities
Rules of Probability
Equally likely outcomes
Combinatorics
Conditional Probability
Independence

Events and their probabilities

A collection of all elementary results, or outcomes of an experiment, is called a sample space.
Any set of outcomes is an event. Thus, events are subsets of the sample space.
A sample space of $N$ possible outcomes yields $2^N$ possible events.
Notation:

\[\Omega = \text{sample space}\]

\[\emptyset = \text{empty event}\]

\[P\{E\} = \text{probability of event E}\]

Example 1

A tossed die can produce one of 6 possible outcomes: 1 dot through 6 dots.

Each outcome is an event.
There are other events:
- observing an even number of dots
- an odd number of dots
- a number of dots less than 3
- etc.

Set Operations

\[A \cup B = \text{union} \quad A \cap B = \text{intersection}\]

\[\overline{A} \text{ or } A^c = \text{complement} \quad A \backslash B = \text{difference}\]

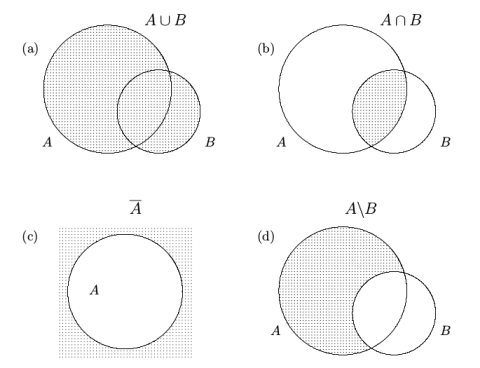
setops

Events: Disjoint, mutually exclusive, exhaustive

Events A and B are disjoint if their intersection is empty,

\[A \cap B = \emptyset\]

Events $A_1, A_2, A_3, \cdots$ are mutually exclusive or pairwise disjoint if any two of these events are disjoint, i.e.,

\[A_i \cap A_j = \emptyset, \text{ for any } i \neq j\]

Events A, B, C are exhaustive if their union equals the whole sample space, i.e.,

\[A \cup B \cup C \cup \cdots = \Omega\]

Example 2

Receiving a grade of A, B, or C for some course are mutually exclusive events, but unfortunately, they are not exhaustive.

De Morgan's laws

the complement of the union of two sets is the same as the intersection of their complements

\[\overline{A \cup B} = \overline{A} \cap \overline{B}\]

the complement of the intersection of two sets is the same as the union of their complements

\[\overline{A \cap B} = \overline{A} \cup \overline{B}\]

Rules of Probability

A collection $\mathfrak{M}$ of events is a sigma-algebra on sample space $\Omega$ if

it includes the sample space,

\[\mathfrak{M} \in \Omega\]

every event in $\mathfrak{M}$ is contained along with its complement; i.e.

\[E \in \mathfrak{M} \Rightarrow \overline{E} \in \mathfrak{M}\]

every finite or countable collection of events in M is contained along with its union; i.e.

\[E_1, E_2, \ldots \in \mathfrak{M} \Rightarrow E_1 \cup E_2 \cup \ldots \in \mathfrak{M}\]

Example 3

This minimal collection $\mathfrak{M} = \{\Omega, \emptyset\}$ forms a sigma-algebra that is called degenerate.
The collection of all the events, $\mathfrak{M} = 2^\Omega = \{E, E \in \Omega\}$ forms a sigma-algebra that is called a power set.
Let sample space $\Omega = \mathbb{R}$, then a sigma-algebra $\mathfrak{B}$, that is called Borel, to be a collection of all the intervals, finite and infinite, open and closed, and all their finite and countable unions and intersections. In fact, it consists of all the real sets that have length.

Axioms of Probability

Assume a sample space $\Omega$ and a sigma-algebra of events $\mathfrak{M}$ on it. Probability is a function of events with the domain $\mathfrak{M}$ and the range [0, 1]

\[P : \mathfrak{M} \rightarrow [0, 1]\]

that satisfies the following two conditions,

Unit measure: The sample space has unit probability,

\[P(\Omega) = 1\]

Sigma-additivity: For any finite or countable collection of mutually exclusive events $E_1, E_2, \ldots \in \mathfrak{M}$,

\[P \{E_1 \cup E_2 \cup \ldots \} = P(E_1) + P(E_2) + \ldots\]

Computing probabilities of events

A sample space $\Omega$ consists of all possible outcomes, therefore, it occurs for sure, $P \{\Omega\} = 1$

On the contrary, an empty event $\emptyset$ never occurs, $P \{\emptyset\} = 0$

Consider an event that consists of some finite or countable collection of mutually exclusive outcomes, $E=\{ \omega_1, \omega_2, \ldots \}$,

\[P \{E\} = \sum_{\omega_k \in E} P\{\omega_k\}\]

Computing probabilities of events (cont.)

Probability of a union

If events are not mutually exclusive (intersect), their probabilities cannot be simply added.

\[P \{A \cup B \} = P \{A\} + P \{B\} - P \{A \cap B \}\]

Complement

Events $A$ and $\overline{A}$ are exhaustive, $A \cup \overline{A} = \Omega$, so

\[P \{\overline{A} \} = 1 - P \{A\}\]

Intersection of independent events

Events $E_1, E_2, \ldots, E_n$ are independent if they occur independently of each other, i.e., occurrence of one event does not affect the probabilities of others.

\[P \{E_1 \cap \ldots \cap E_n \} = P \{ E_1 \} \cdot \ldots P \{ E_n \}\]

There is a 1% probability for a hard drive to crash. Therefore, it has two backups, each having a 2% probability to crash, and all three components are independent of each other. The stored information is lost only in an unfortunate situation when all three devices crash. What is the probability that the information is saved?

Equally likely outcomes

When the sample space $\Omega$ consists of $n$ possible outcomes, $\omega_1, \ldots, \omega_n$, each having the same probability.

Since $P(\Omega) = 1$, then $P(\omega_k) = 1/n$ for all $k$.

Further, a probability of any event $E$ consisting of $t$ outcomes, equals

\[P \{E\} = \sum_{\omega_k \in E} \left(\frac{1}{n}\right) = t\left(\frac{1}{n}\right) = \frac{\#\text{ of favorable outcomes}}{\# \text{ of total outcomes}}\]

Example 5

Tossing a die results in 6 equally likely possible outcomes, identified by the number of dots from 1 to 6.

P {1} = ?
P { odd number of dots } = ?
P { less than 5 } = ?

Combinatorics

Sampling with replacement means that every sampled item is replaced into the initial set, so that any of the objects can be selected with probability 1/n at any time. In particular, the same object may be sampled more than once.

Permutations with replacement

\[P_r(n, k) = n^k\]

Permutations

Sampling without replacement means that every sampled item is removed from further sampling, so the set of possibilities reduces by 1 after each selection.

Permutations without replacement

\[P(n, k) = \frac{n!}{(n-k)!}\]

Combinations

Combinations with replacement

\[C_r(n, k) = \binom{k+n-1}{k} = \frac{(k+n-1)!}{k!(n-1)!}\]

Combinations without replacement

\[C(n, k) = \binom{n}{k} = \frac{n!}{k!(n-k)!}\]

Conditional probability

Conditional probability of event $A$ given event B is the probability that $A$ occurs when $B$ is known to occur.

\[P \{A \;|\; B\} = \text{conditional probability of A given B}\]

\[P \{A \;|\; B\} = \frac{\#\text{ of outcomes in } A \cap B}{\# \text{ of outcomes in } B} = \frac{ P\{A \cap B\}}{ P\{B\}}\]

Independence

Events $A$ and $B$ are independent if occurrence of $B$ does not affect the probability of $A$, i.e.,

\[P \{A \;|\; B\} = P \{A\}\]

Example 6

Ninety percent of flights depart on time. Eighty percent of flights arrive on time. Seventy-five percent of flights depart on time and arrive on time.

You are meeting a flight that departed on time. What is the probability that it will arrive on time?
You have met a flight, and it arrived on time. What is the probability that it departed on time?
Are the events, departing on time and arriving on time, independent?

Bayes Rule

Because $A \cap B = B \cap A$, thus

\[P \{B \;|\; A\} = \frac{ P\{A \;|\; B\}P\{B\}}{ P\{A\} }\]

Example 7

On a midterm exam, students X, Y , and Z forgot to sign their papers. Professor knows that they can write a good exam with probabilities 0.8, 0.7, and 0.5, respectively. After the grading, he notices that two unsigned exams are good and one is bad. Given this information, and assuming that students worked independently of each other, what is the probability that the bad exam belongs to student Z?

Law of Total Probability

Consider some partition of the sample space $\Omega$ with mutually exclusive and exhaustive events $B_1 , \ldots, B_k$. It means that

\[B_i\cap B_j = \emptyset, \; \forall i\neq j \text{ and } B_1 \cup \ldots \cup B_k = \Omega\]

These events also partition the event $A$,

\[A = (A \cap B_1) \cup \ldots \cup (A \cap B_k)\]

Hence,

\[P\{A\} = \sum_{j=1}^k P \{ A \;|\; B_j\} P\{B_j\}\]

Example 8

There exists a test for a certain viral infection (including a virus attack on a computer network). It is 95% reliable for infected patients and 99% reliable for the healthy ones. Suppose that 4% of all the patients are infected with the virus. If the test shows positive results, what is the probability that a patient has the virus?