Statistics

Statistics

Variable Types

Example 1

Population and Sample

A population consists of all units of interest. Any numerical characteristic of a population is a parameter, $\theta$.

A sample consists of observed units collected from the population. It is used to make statements about the population. Any function of a sample is called statistic.

In order to know the population parameters, one must measure the entire population, i.e., to conduct a census.

Parameters

Parameters can be estimated a form of a random population sample up to a certain measurable degree of accuracy.

params-stats.png

Errors

Sampling errors are caused by the mere fact that only a sample, a portion of a population, is observed.

Non-sampling errors are caused by inappropriate sampling schemes or wrong statistical techniques.

Sampling Designs

Simple Random Sample (SRS)

A sample drawn so that every possible sample has an equal chance of being selected is called a simple random sample.

Stratified Sampling

Reduced sampling variability is the most important benefit of stratifying.

Cluster and Multistage Sampling

Clustering sampling

Multistage samples

Systematic Samples

Example 2

Researchers waited outside a bar they had randomly selected from a list of such establishments. They stopped every 10th person who came out of the bar and asked whether he or she thought drinking and driving was a serious problem. Identify the population of interest, population parameter, sampling frame and method.

Example 2 (cont.)

Example 3

An amusement park has opened a new roller coaster. It is so popular that people are waiting for up to 3 hours for a 2-minute ride. Concerned about how patrons feel about this, they survey every 10th person on the line for the roller coaster, starting from a randomly selected individual. Identify sampling frame. Is the sample likely to be representative?

Example 3 (cont.)

Bad Sampling

Voluntary Response Sample

Convenience Sampling

Bad Sampling Frame

An SRS from an incomplete sampling frame introduces bias because the individuals included may differ from the ones not in the frame.

Undercoverage

Example 4

We want to know what percentage of local doctors accept Medicaid patients. We call the offices of 50 doctors randomly selected from local Yellow Pages listings. Is this sampling method appropriate? If not, identify the problem.

Is this method appropriate?

Example 4 (cont.)

We want to know what percentage of local doctors accept Medicaid patients. We call the offices of 50 doctors randomly selected from local Yellow Pages listings. Is this sampling method appropriate? If not, identify the problem.

Method appropriate: Depends on the Yellow Page listing used. If from regular listings, this is fair if all doctors are listed. If from ads, then probably not as those doctors may not be typical.

Simple Descriptive Statistics

Shape

When you describe a distribution, you should pay attention to its:

We describe the shape of a distribution in terms of its modes, its symmetry, and whether it has any gaps or outlying values.

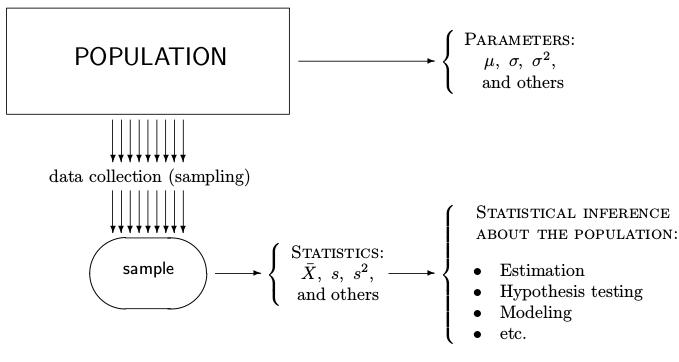
Mode

Peaks or humps seen in a histogram are called the modes of a distribution.

A distribution whose histogram has

modes

Symmetry

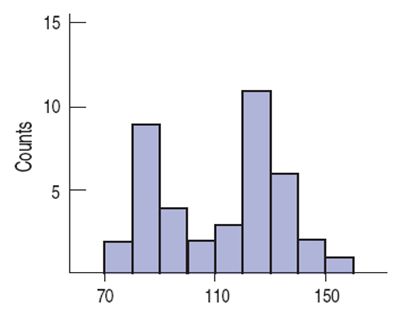
A distribution is symmetric if the halves on either side of the center look, at least approximately, like mirror images.

The thinner ends of a distribution are called the tails. If one tail stretches out farther than the other, the distribution is said to be skewed to the side of the longer tail.

tail

Outliers

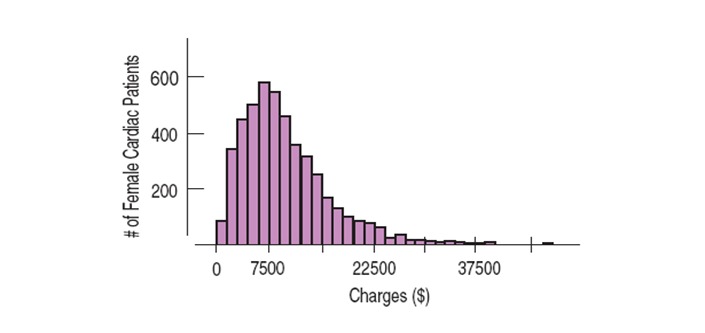
The outliers in a distribution are those values that stand off away from the body of the distribution.

Mean

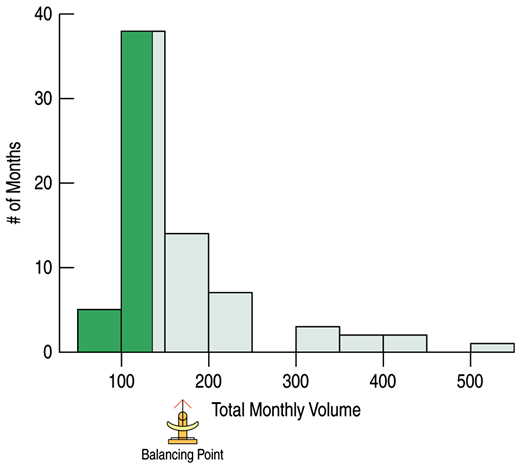
The mean of a distribution is calculated as sum of all values, $X_i$, and divided by the number of values, $N$.

\[\bar{X} = \frac{\sum_{i=1}^N X_i}{N}\]

The mean is considered to be the balancing point of the distribution.

Bias

An estimator $\hat{\theta}$ is unbiased for a parameter $\theta$ if its expectation equals the parameter, $E(\hat{\theta}) = \theta$ for all possible values of $\theta$.

Bias of $\hat{\theta}$ is defined as $Bias(\hat{\theta}) = E(\hat{\theta}) - \theta$

Consistency

An estimator $\hat{\theta}$ is consistent for a parameter $\theta$ if the probability of its sampling error of any magnitude converges to 0 as the sample size increases to infinity, $P\{ |\hat{\theta} - \theta| > \varepsilon \} \rightarrow 0, \; n \rightarrow \infty$

for any $\varepsilon > 0$.

That is, when we estimate $\theta$ from a large sample, the estimation error $|\hat{\theta} - \theta|$ is unlikely to exceed $\varepsilon$, and it does it with smaller and smaller probabilities as we increase the sample size, $n$.

Asymptotic Normality

By the Central Limit Theorem, the sum of observations, and therefore, the sample mean have approximately Normal distribution if they are computed from a large sample. That is, the distribution of

\[Z = \frac{\bar{X} - E(\bar{X})}{ Std(\bar{X})} = \frac{\bar{X} - \mu}{ \sigma \sqrt{n} }\]

converges to Standard Normal as $n \rightarrow \infty$. This property is called Asymptotic Normality.

Median

The median is the value separating the higher half the data from lover part.

The median is resistant to unusual observations and to the shape of the distribution.

median

Spread

Sometimes we need to determine how spread out the data.

One simple measure of spread is the range, defined as the difference between the extremes.

\[R = \max - \min\]

The range is a single value and it is not resistant to unusual observations.

Quantile

A $p$-quantile of a population is such a number x that solves equations $ \begin{cases} P{X < x} \leq p \ P{X > x} \leq 1-p \end{cases} $

A sample $p$-quantile is any number that exceeds at most $100p$% of the sample, and is exceeded by at most $100(1 - p)$% of the sample.

A $\gamma$-percentile is $(0.01\gamma)$-quantile.

Quartiles

The quartiles of a ranked set of data values are the three points that divide the data set into four equal groups, each group comprising a quarter of the data.

Interquartile Range

The interquartile range (IQR) is defined to be the difference between the two quartile values.

\[IQR = Q_3 - Q_1\]

Variance

For a sample $(X_1, \ldots, X_n)$, the average of the squared deviations of the values of the variable $X_i$ from the mean, $\bar{X}$, is called the sample variance and is denoted by $s^2$.

\[s^2 = \frac{1}{n-1}\sum_{i=1}^n (X_i-\bar{X})^2\]

It measures variability among observations and estimates the population variance, $\sigma^2 = Var(X)$.

Taking the square root of the variance corrects this issue and gives us the standard deviation.

Standard error of an estimator $\hat{\theta}$ is its standard deviation, $\sigma(\hat{\theta}) = Std(\hat{\theta})$.

Guide

Graphical statistics

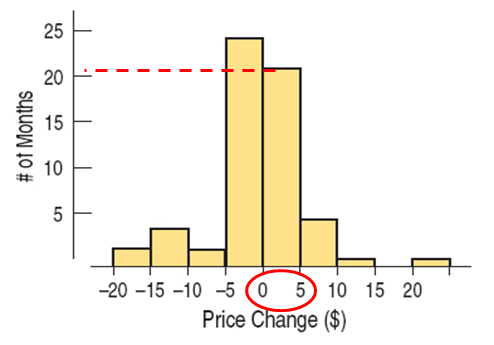
Histograms

A histogram is similar to a bar chart with the bin counts used as the heights of the bars. Note: there are no gaps between bars unless there are actual gaps in the data.

histogram

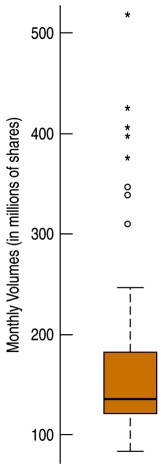
Boxplot

The five-number summary of a distribution reports its median, quartiles, and extremes (maximum and minimum).

boxplot

Boxplot (cont)

Example

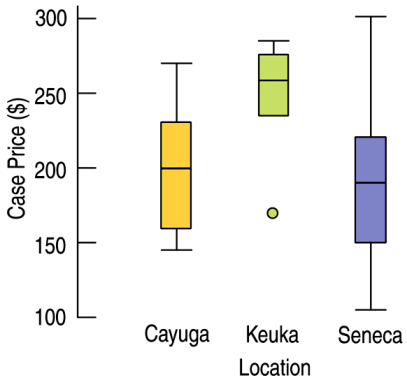
Example: Wine Prices The boxplots displayed case prices (in dollars) of wines produces by vineyards along three of the Finger Lakes in upstate New York.

  1. Which lake region produces the most expensive wine?

  2. Which lake region produces the cheapest wine?

  3. In which region are wines generally more expensive?

winebox

Example (cont.)

  1. Seneca Lake

  2. Seneca Lake

  3. Keuka Lake

Cayuga Lake vineyards and Seneca Lake have approximately the same average case price of about 200, while a typical Keuka Lake vineyard has a case price of about 260. Keuka Lake vineyards have consistently high case prices, between 240 and 280, with one low outlier at about 170 per case. Cayuga Lake vineyards have case prices from 140 to 270, and Seneca Lake vineyards have highly variable case prices from 100 to 300.

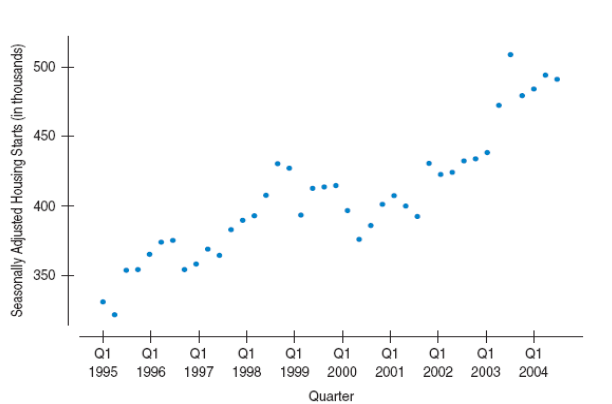
Scatterplot

Scatterplots are the ideal way to picture associations between two quantitative variables.

scatter

Other

Example: Create a stem-and-leaf display for the data 21, 22, 24, 33, 33, 36, 38, 41.

2|124
3|3368
4|1