Discrete Random Variables and Their Distributions

Discrete Random Variables and Their Distributions

Random Variables

Example 1

Consider an experiment of tossing 3 fair coins and counting the number of heads.

Let $X$ be the number of heads. Prior to an experiment, its value is not known. All we can say is that $X$ has to be an integer between 0 and 3. Since assuming each value is an event, we can compute probabilities,

\[P\{X = 0\} = P\{TTT\} =1/2 \cdot 1/2 \cdot 1/2 = 1/8\]
\[P\{X = 1\} = P\{HTT\} + P\{THT\} + P\{TTH\}= 3/8\]
\[P\{X = 2\} = P\{HHT\} + P\{HTH\} + P\{THH\}= 3/8\]
\[P\{X = 3\} = P\{HHH\} = 1/8\]

Discrete Distribution

Collection of all the probabilities related to $X$ is the distribution of X. The function $P(x) = P\{X=x\}$ is the probability mass function, or pmf.

The cumulative distribution function, or cdf is defined as $F(x) = P\{X \leq x\} = \sum_{y\leq x}P(y)$

The set of possible values of $X$ is called the support of the distribution $F$.

Distribution probabilities

For any set $A$,

\[P\{X \in A\} = \sum_{x \in A} P(x)\]

When $A$ is an interval, its probability can be computed directly from the cdf $F(x)$, $P \{a < X \leq b\} = F(b) - F(a)$

Example 2

A program consists of two modules. The number of errors $X_1$ in the first module has the pmf $P_1(x)$, and the number of errors $X_2$ in the second module has the pmf $P_2(x)$, independently of $X_1$, if

x$P_1(x)$$P_2(x)$
00.50.7
10.30.2
20.10.1
30.10.0

Find the pmf and cdf of $Y = X_1 + X_2$, the total number of errors.

Joint and marginal distributions

Joint probability distribution

\[P(x,y) = P\{(X,Y) = (x,y)\} = P\{X = x \cap Y = y\}\]
\[\sum_x \sum_y P(x,y) = 1\]

Addition Rule

\[P_X(x) = P\{X = x\} = \sum_y P_{(X,Y)}(x,y)\]
\[P_Y(y) = P\{Y = y\} = \sum_x P_{(X,Y)}(x,y)\]

Independence

Random variables $X$ and $Y$ are independent if

\[P_{(X,Y)}(x,y) = P_X(x) P_Y(y)\]

for all values of $x$ and $y$.

This means, events $\{X = x\}$ and $\{Y = y\}$ are independent for all $x$ and $y$.

Example 3

A program consists of two modules. The number of errors, $X$, in the first module and the number of errors, $Y$, in the second module have the joint distribution, $P(0, 0) = P(0, 1) = P(1, 0) = 0.2$, $P(1, 1) = P(1, 2) = P(1, 3) = 0.1$, $P(0, 2) = P(0, 3) = 0.05$. Find:

  1. the marginal distributions of $X$ and $Y$

  2. the probability of no errors in the first module

  3. the distribution of the total number of errors in the program

  4. find out if errors in the two modules occur independently.

Expectation and Variance

Expectation or expected value of a random variable $X$ is its mean, the average value. It's denoted by $E[X]$, and defined by

\[E[X] = \sum_x x P(X=x)\]

Properties of Expectations

For any random variables $X$ and $Y$ and any non-random numbers $a$ and $c$ $E(X + Y) = E(X) + E(Y)$ $E(aX) = a E(X)$ $E(c) = c$

For independent $X$ and $Y$, $E(XY) = E(X)E(Y)$

Example 4

What are the expected values of $X$, $Y$, and $X+Y$ from Ex. 3?

Variance

Variance of a random variable is defined as the expected squared deviation from the mean. For discrete random variables, variance is

\[\sigma^2 = Var(X) = E[(X - E[X])^2] = \sum_x (x - \mu)^2 P(x)\]

or

\[Var(X) = E[X^2] - \mu^2\]

Standard Deviation

Standard deviation is a square root of variance $\sigma = Std(X) = \sqrt{Var(X)}$

Covariance

Covariance is the expected product of deviations of $X$ and $Y$ from their respective expectations, which summarizes interrelation of two random variables.

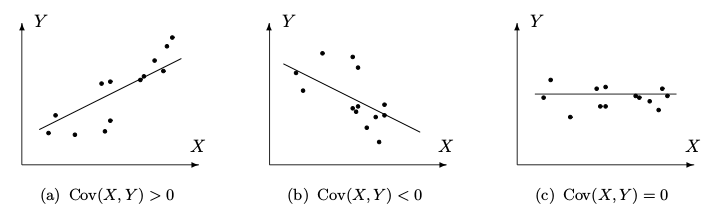
covariance

Covariance $\sigma_{XY} = Cov(X,Y)$ is defined as

\[Cov(X,Y) = E[(X-E[X])(Y-E[Y])]\]
\[= E[XY]-E[X]E[Y]\]

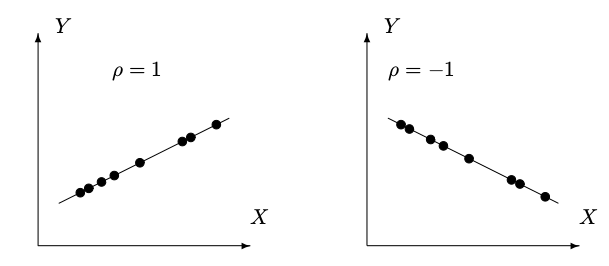
Correlation

If $Cov(X,Y)=0$, we say that $X$ and $Y$ are uncorrelated.

Correlation coefficient between variables $X$ and $Y$ is defined as

\[\rho = \frac{Cov(X,Y)}{\sigma_X \sigma_Y}\]

Correlation coefficient is a rescaled, normalized covariance.

correlation

Properties of Variances and Covariances

\[Var(aX + bY + c) = a^2 Var(X) + b^2 Var(Y) + 2ab Cov(X,Y)\]
\[Cov(aX + bY, cZ+dW)= acCov(X, Z) +\]
\[adCov(X, W ) + bcCov(Y, Z) + bdCov(Y,W)\]
\[Var(aX + b) = a^2 Var(X)\]
\[Cov(aX + b, cY + d) = acCov(X, Y)\]
\[\rho(aX + b, cY + d) = \rho(X,Y)\]
\[Cov(X,Y) = Cov(Y,X), \; \rho(X,Y) = \rho(Y,X)\]

For independent $X$ and $Y$,

\[Cov(X,Y) = 0, \; Var(X + Y) = Var(X) + Var(Y)\]

Example 5

What are the variance, std. deviation, covariance, and correlation values of $X$, $Y$, and $X+Y$ from Ex. 3?

Chebyshev's Inequality

Any random variable $X$ with expectation $\mu = E(X)$ and variance $\sigma^2 = Var(X)$ belongs to the interval $\mu \pm \varepsilon$ with probability of at least $1-(\sigma/\varepsilon)^2$ . That is

\[P\{|X-\mu| > \varepsilon\} \leq \left(\frac{\sigma}{\varepsilon}\right)^2\]

for any distribution with expectation $\mu$ and variance $\sigma^2$ and for any positive $\varepsilon$.

Example 6

Suppose the number of errors in a new software has expectation $\mu = 20$ and a standard deviation of 2.

Discrete Distributions

Bernoulli Distribution

A random variable with two possible values, 0 and 1, is called a Bernoulli variable, its distribution is Bernoulli distribution, and any experiment with a binary outcome is called a Bernoulli trial.

\[E(X) = \sum_x P(x) = 0(1-p) + (1)(p) = p\]
\[Var(X) = \sum_x (x-p)^2 P(x) = (0-p)^2(1-p)+(1-p)^2p =\]
\[= p(1-p) = pq\]

Binomial Distribution

A variable described as the number of successes in a sequence of independent Bernoulli trials has Binomial distribution. Its parameters are $n$, the number of trials, and $p$, the probability of success.

\[P(x) = P\{X=x\} = \binom{n}{x} p^x q^{n-x}, \; x=0,1,\ldots,n\]

Binomial Distribution: Expectation and Variance

Any Binomial variable $X$ can be represented as a sum of independent Bernoulli variables,

\[X = X_1 + \cdots + X_n\]

Thus, Binomial expectation and variance can be calculated as follows

\[E(X) = E(X_1 + \cdots + X_n) = E(X_1) + \cdots + E(X_n)\]
\[= p + \ldots + p = np\]
\[Var(X) = Var(X_1 + \cdots + X_n) = Var(X_1) + \cdots + Var(X_n)\]
\[= npq\]

Example 7

An exciting computer game is released. Sixty percent of players complete all the levels. Thirty percent of them will then buy an advanced version of the game. Among 15 users, what is the expected number of people who will buy the advanced version?

Example 8

Consider the situation of a multiple-choice exam. It consists of 10 questions, and each question has four alternatives (of which only one is correct).

Geometric Distribution

The number of Bernoulli trials needed to get the first success has Geometric distribution.

\[P(x) = P\{ \text{the 1st success occurs on x-th trial} \} = (1-p)^{x-1} p\]

for $x=1,2, \ldots$

\[E(X) = \sum_{x=1}^\infty x q^{x-1}p = \frac{1}{(1-q)^2}p = \frac{1}{p}\]
\[Var(X) = \frac{1-p}{p^2}\]

Example 9

A driver looking for at a parking space down the street. There are five cars in front of the driver, each of which having a probability 0.2 of taking the space.

Poisson Distribution

The number of rare events occurring within a fixed period of time has Poisson distribution.

\[P(x) = e^{-\lambda}\frac{\lambda^x}{x!}, \; x=0,1,2,\ldots\]
\[E(X) = \lambda\]
\[Var(X) = \lambda\]

Example 10

Customers of an internet service provider initiate new accounts at the average rate of 10 accounts per day.

Poisson Approximation of Binomial Distribution

Poisson distribution can be effectively used to approximate Binomial probabilities when the number of trials $n$ is large, and the probability of success $p$ is small.

\[Binomial(n,p) \approx Poisson(\lambda)\]
\[\text{where } n \ge 30, p \le 0.05, np = \lambda\]

Example 11

Ninety-seven percent of electronic messages are transmitted with no error.