Lecture 4

Outline

Random Variable Statistics
Discrete Probability Models

Random Variable Statistics

A variable whose value is based on the outcome of a random event is called a random variable.
If we can list all possible outcomes, the random variable is called a discrete random variable.
If a random variable can take on any value between two values, it is called a continuous random variable.

Expected Value of a Random Variable

For both discrete and continuous random variables, the set of all the possible values and their associated probabilities is called the probability model.
When the probability model is known, then the expected value can be calculated:

\[E(X) = \sum_X x \cdot P(x)\]

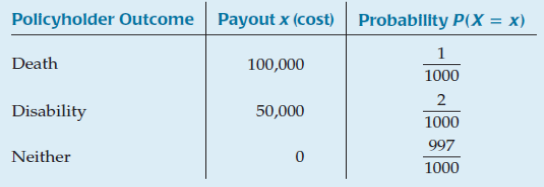
Example 1

Find the expected annual payout on a policy.

rv-exp

Standard Deviation of a Random Variable

Standard Deviation of a discrete random variable:

\[\sigma^2 = Var(X) = \sum_X (x-\mu)^2 \cdot P(x)\]

\[\sigma = SD(X) = \sqrt Var(X)\]

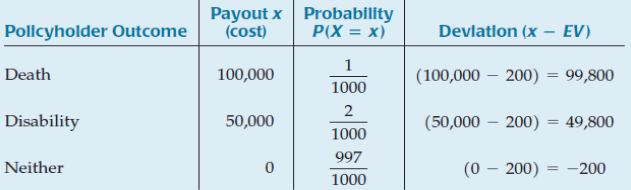
Example 2

Find the standard deviation of the annual payout.

rv-var

Example 3

Suppose the probabilities of a customer purchasing 0, 1, or 2 books at a book store are 0.2, 0.4 and 0.4 respectively.

What is the expected number of books a customer will purchase?
What is the standard deviation of the book purchases?

Properties of Expected Values and Variances

Adding a constant $c$ to $X$:

\[E(X \pm c) = E(X) \pm c\]

\[Var(X \pm c) = Var(X)\]

\[SD(X \pm c) = SD(X)\]

Multiplying $X$ by a constant $c$:

\[E(cX) = cE(X)\]

\[Var(cX) = c^2Var(X)\]

\[SD(cX) = |c|SD(X)\]

Properties of Expected Values and Variances (cont.)

Addition Rule for Expected Values of Random Variables

\[E(X \pm Y) = E(X) \pm E(Y)\]

Addition Rule for Variances of (independent) Random Variables

\[Var(X \pm Y) = Var(X) + Var(Y)\]

\[SD(X + Y) = \sqrt \{Var(X) + Var(Y)\}\]

Example 3

The expected annual payout per insurance policy is 200 and the variance is 14,960,000.

If the payout amounts are doubled, what are the new expected value and variance?

Compare this to the expected value and variance on two independent policies at the original payout amount.

Discrete Probability Models

The Uniform Model

If $X$ is a random variable with possible outcomes 1, 2, ..., n and $P(X=i) = 1/n$ for each $i$, then we say $X$ has a discrete Uniform distribution, U[1, ..., n].

Example: a fair die

U[1,2,3,4,5,6] with $P(X=i) = 1/6$

Bernoulli Trials

A Bernoulli Trial is a trial with the following characteristics:

There are only two possible outcomes (success and failure) for each trial.
The probability of success, denoted $p$, is the same for each trial. The probability of failure is $q = 1 - p$.
The trials are independent.

The Geometric Model

Predicting the number of Bernoulli trials required to achieve the first success.

Probability of success: $p$
Condition: X = number of trials until the first success occurs

\[P(X=x) = q^{x-1}p\]

Expected value: $E(X) = \frac{1}{p}$
Standard deviation: $SD(X) = \sqrt \frac{q}{p^2}$

Example 4

Find the mean (expected value) of a random variable $X$, using a geometric distribution with probability of success, p.

X	0	1
P(X)	q	p

Independence

Bernoulli Trials must be independent.
The 10% Condition: From finite populations, the sample should be no more than 10% of the population.

The Binomial Model

Predicting the number of successes in a fixed number of Bernoulli trials.

Number of trials: $n$
Probability of success: $p$
Condition: X = number of successes in $n$ trials

\[P(X=x) = \binom{n}{x} p^x q^{n-x}, \binom{n}{x} = \frac{n!}{x!(n-x)!}\]

Expected value: $E(X) = np$
Standard deviation: $SD(X) = \sqrt npq$

The Poisson Model

Predicting the number of events that occur over a given interval of time or space.

Mean number of occurrences: $\lambda$
Condition: X = number of occurrences

\[P(X=x) = \frac{e^{-\lambda}\lambda^x}{x!}\]

Expected value: $E(X) = \lambda$
Standard deviation: $SD(X) = \sqrt \lambda$

Example 6

For example, a website averages 4 hits per minute. Find the probability that there will be no hits in the next minute.

Example 7

A salesman normally closes a sale on 80% of his presentations. Assuming the presentations are independent:

What model should be used to determine the probability that he closes his first presentation on the fourth attempt? Geometric
What is the probability he closes his first presentation on the fourth attempt?

\[P(X=3)=(0.2)^3(0.8)=0.0064\]

Example 8

A tennis player makes a successful first serve 67% of the time. Of the first 6 serves of the next match:

What model should be used to determine the probability that all 6 first serves will be in bounds? Binomial
What is the probability that all 6 first serves will be inbounds?

\[P(X=6)=\binom{6}{6}(0.67)^6(0.33)^0=0.0905\]

How many first serves can be expected to be inbounds?

\[E(X) = np = 6(0.67) =4.02\]

A cable provider wants to contact customers to see if they are satisfied with a new digital TV service. If all customers are in the 452 phone exchange, (so there are 10,000 possible numbers from 452-0000 to 452-9999)

What probability model would be used to model the selection of a single number? Uniform, all numbers are equally likely.
What is the probability the number selected will be an even number? 0.5
What is the probability the number selected will end in 000? 0.001

Example 10

A website manager has noticed that during evening hours, about 3 people per minute make an online purchase. She believes that each purchase is independent of the others.

What probability model would be used to model the number of purchases per minute? Poisson
What is the probability that in any one minute at least one purchase is made?

\[P(X\ge1) = 1 - P(X=0) = 1 - \frac{e^{-3}3^0}{0!} = 0.9502\]

What is the probability that no one makes a purchase in the next 2 minutes?

\[P(X=0)=\frac{e^{-6}6^0}{0!} = 0.00248\]