Lecture 9
Outline
Inference for Counts: Chi-Square Tests
Goodness-of-Fit Tests
Given the following
Counts of items in each of several categories
A model that predicts the distribution of the relative frequencies
How good is the fit?
Does the actual distribution differ from the model because of random error,
or do the differences mean that the model does not fit the data?
Assumptions and Condition
Counted Data Condition: The data must be counts for the categories of a categorical variable.
Independence Assumption: The counts should be independent of each other. Think about whether this is reasonable.
Randomization Condition: The counted individuals should be a random sample of the population. Guard against auto-correlated samples.
Sample Size Assumption: There must be enough data so check the following condition.
Expected Cell Frequency Condition: Expect at least 5 individuals per cell.
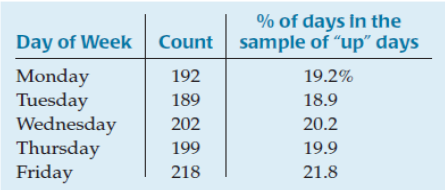
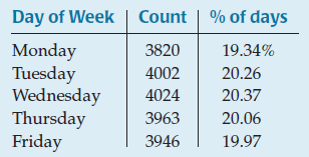
Example 1
| | | |-|-| | |
| |
|
"Up" days appear to be more common than expected on certain days, especially on Fridays.
Null Hypothesis: The distribution of "up" days is no different from the population distribution.
Test the hypothesis with a chi-square goodness-of-fit test.
Chi-Square Model
To decide if the null model is plausible, look at the differences between the observed values and the values expected if the model were true.
So, $\chi^2$ gets “big” when
the data set is large and/or
the model is a poor fit.
The Chi-Square Calculation
Find the expected values. These come from the null hypothesis model. Every null model gives a hypothesized proportion for each cell. The expected value is the product of the total number of observations times this proportion.
Example 1 (cont.)
There were 3820 Mondays out of 19,755 trading days.
So, we'd expect there would be 1000 * 3820/19755 or 193.369 Mondays among the 1000 "up" days.
The Chi-Square Calculation (cont.)
Compute the residuals. Once you have expected values for each cell, find the residuals, $Obs-Exp$.
Square the residuals, $(Obs-Exp)^2$.
Compute the components. Find for each cell, $(Obs-Exp)^2/Exp$
Find the sum of the components. That’s the chi-square statistic,
The Chi-Square Calculation (cont.)
Find the degrees of freedom. It’s equal to the number of cells minus one.
Test the hypothesis. Large chi-square values mean lots of deviation from the hypothesized model, so they give small P-values. Look up the critical value from a table of chi-square values, or find the P-value directly.
Example 2
At a major credit card bank, the percentages of people who historically apply for the Silver, Gold, and Platinum cards are 60%, 30%, and 10% respectively. In a recent sample of customers, 110 applied for Silver, 55 for Gold, and 35 for Platinum. Is there evidence to suggest the percentages have changed?
What type of test do you conduct? This is a goodness-of-fit test comparing a single sample to previous information (the null model).
Example 2 (cont.)
What are the expected values?
| Values | Silver | Gold | Platinum |
|---|---|---|---|
| Observed | 110 | 55 | 35 |
| Expected | 120 | 60 | 20 |
Find the test statistic and P-value.
Using df = 2, the P-value < 0.005
Reject the null hypothesis. There is sufficient evidence customers are not applying for cards in the traditional proportions.
Interpreting Chi-Square Values
The $\chi^2$ distribution is right-skewed and becomes broader with increasing degrees of freedom:
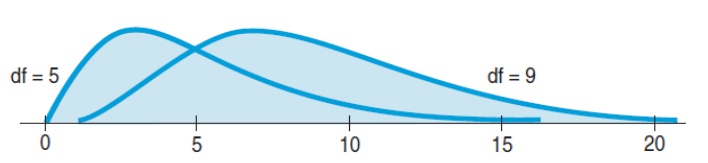
The expected value of $\chi^2$ model is its number of degrees of freedom.
The $\chi^2$ test is a one-sided test.
Examining the Residuals
When we reject a null hypothesis, we can examine the residuals in each cell to discover which values are extraordinary.
Because we might compare residuals for cells with very different counts, we should examine standardized residuals:
Note that standardized residuals from goodness-of-fit tests are actually z-scores.
The Chi-Square Test for Homogeneity
How important is it to seek your utmost attractive appearance?
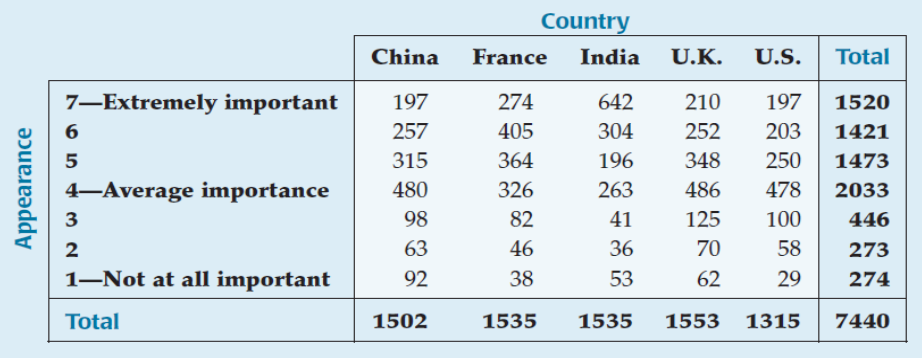
The Chi-Square Test for Homogeneity (cont.)
Convert the results to "column percentages":
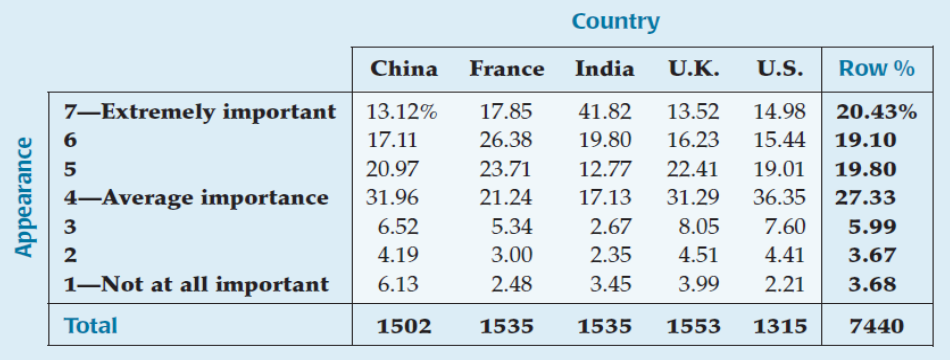
The Chi-Square Test for Homogeneity (cont.)
It seems that India stands out from the others.
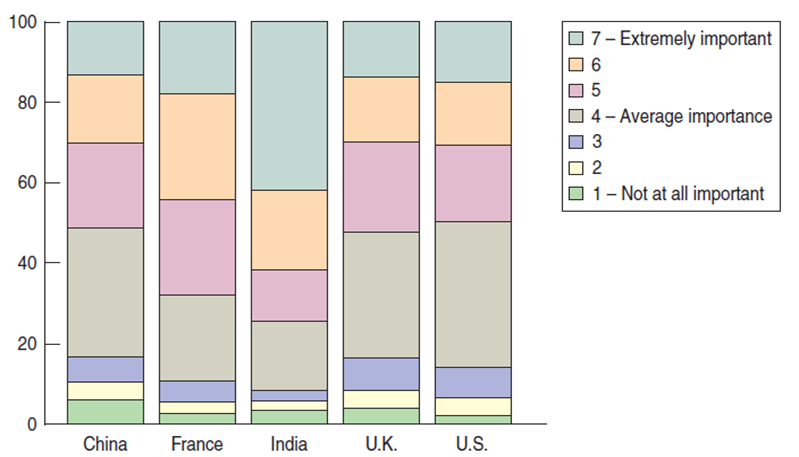
Our null hypothesis is that the relative frequency distributions are homogeneous for each country.
Test the hypothesis with a chi-square test for homogeneity.
The Chi-Square Test for Homogeneity (cont.)
Counted Data Condition: Data must be counts
Independence Assumption: Counts need to be independent from each other.
Randomization Condition: Random sample needed
Sample Size Assumption: There must be enough data so check the following condition.
Expected Cell Frequency Condition: Expect at least 5 individuals per cell.
The Chi-Square Test for Homogeneity (cont.)
Use the Row % column to determine the expected counts for each table column (each country)
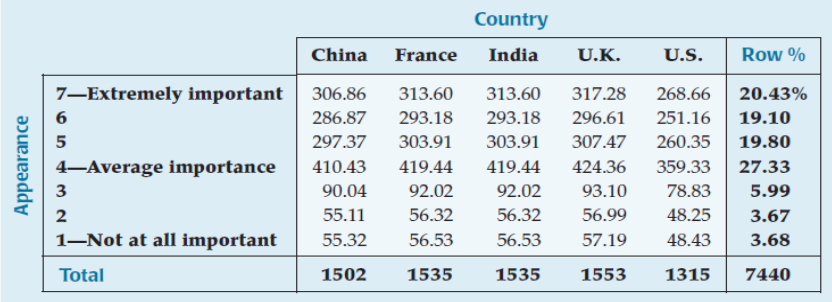
The Chi-Square Test for Homogeneity (cont.)
Following the pattern of the goodness-of-fit test, we compute the component for each cell of the table:
Summing these components across all cells gives $\chi^2$:
For a test of homogeneity, there are degrees of freedom, $(R-1)\times(C-1)$ where $R$ is the number of rows and $C$ is the number of columns.
Comparing Two Proportions
Are women more likely to graduate high school than men, or are the differences due to random variation?
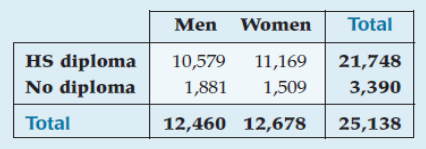
Men: 84.9% diploma rate
Women: 88.1% diploma rate
Overall 86.5% of the sample had diplomas.
Use this proportion to compute the expected values.
Comparing Two Proportions (cont.)
| Observed Counts | Expected Values |
|---|---|
 | 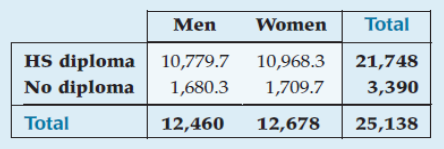 |
The chi-square statistic with (2-1)*(2-1) = 1 df is
This has a P-value < 0.001, so we reject the null hypothesis
Conclude that the distribution of receiving high school diplomas is different for men and women.
A chi-square test with 1 df, is equivalent to testing whether two proportions are equal.
Chi-Square Test of Independence
Are Age and Appearance independent, or is there a relationship?
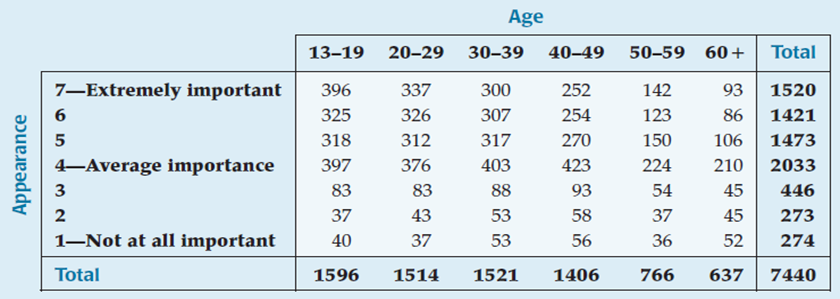
Chi-Square Test of Independence (cont.)
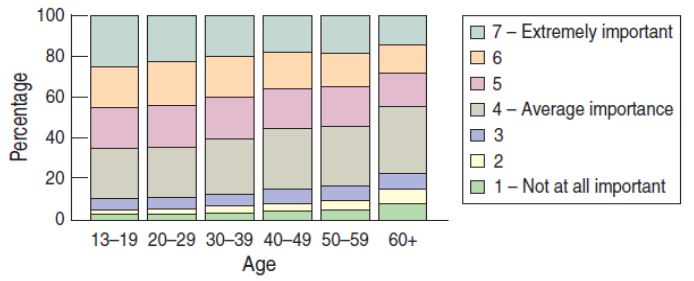
Test for independence using a chi-square test of independence.
Chi-Square Test of Independence (cont.)
The test is mechanically equivalent to the test for homogeneity, but with some differences in how we think about the data and the results:
Homogeneity Test: one variable (Appearance) measured on two or more populations (countries).
Independence Test: Two variables (Appearance and Age) measured on a single population.
Chi-Square Test of Independence (cont.)
Counted Data Condition: Data must be counts
Independence Assumption: Counts need to be independent from each other. Check for randomization.
Randomization Condition: Random sample needed
Sample Size Assumption: There must be enough data so check the following condition.
Expected Cell Frequency Condition: Expect at least 5 individuals per cell.
Chi-Square Test of Independence (cont.)
For the Appearance and Age example, we reject the null hypothesis that the variables are independent.
So, it may be of interest to know how differently two age groups select the "very important" category (Appearance response 6 or 7).
Chi-Square Test of Independence (cont.)
Construct a confidence interval for the true difference in proportions
Teens: 45.17%
30-39: 39.91%
The 95% confidence interval is found below:
= from 1.8% to 8.7%
This is a statistically significant difference, but now we can see that the difference may be as small as 1.8%.
Example 3
Consumer Reports uses surveys to measure reliability in automobiles. Annually they release survey results about problems that consumers have had with vehicles in the past 12 months and the origin of manufacturer. Is consumer satisfaction related to country of origin?
State the hypotheses.
Find the test statistic.
Given p-value = 0.231, state your conclusion.
Example 3 (cont.)
State the hypotheses.
- \[H_0\]
, Personal Appearance and Age are independent.
- \[H_A\]
, Personal Appearance and Age are not independent.
Find the test statistic.
Given p-value = 0.231, state your conclusion.
There is not enough evidence to conclude there is an association between vehicle problems and origin of vehicle.